Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 8.Exercícios e Problemas - Ex. 14
14. O peso dos passageiros de uma montanha-russa aumenta em quando o vagão passa pela parte baixa do trilho que corresponde a um arco de círculo com de raio. Quanto vale a velocidade do vagão no fundo do arco?
Passo 1
Opa! Vamos lá resolver mais um problema sobre dinâmica em movimento circular.
Olha só! A seguinte imagem abaixo retrata perfeitamente a situação do nosso problema...
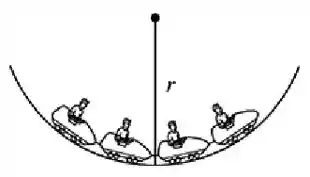
Bom! Quando o carrinho passa pelo ponto mais baixo, temos duas forças atuando sobre ele... Que são a força peso e a força de reação normal pela parte mais baixa do trilho.
Desse modo, chegamos ao seguinte diagrama de corpo...
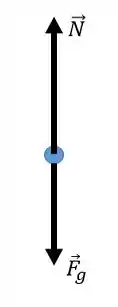
Onde adotamos o modelo do carrinho como partícula pra fazer a representação das nossas forças.
Passo 2
Sendo assim, fazendo a resultante das forças na direção radial, obtemos que...
Agora olha só! Se a questão disse que o peso dos passageiros de uma montanha-russa aumentou em , na real não foi a força peso em si que aumentou. Mas sim, a força de reação normal dos trilhos. De modo que obtemos que,
E substituindo os valores numéricos que temos,
Obtemos finalmente o valor da velocidade no fundo do arco!