Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 27.1 - Ex. 45
Uma casca cilíndrica longa, reta e de parede fina de raio R carrega uma corrente I paralela ao eixo central da casca. Encontre o campo magnético (incluindo a direção) dentro e fora da concha.
Passo 1
Eae galera! Tudo tranquilo? Tendo uma visão geral da coisa, podemos aplicar a lei de Ampère a um círculo centrado no eixo do cilindro e avaliar esta expressão para r
Passo 2
Vamo lá. Aplique a lei de Ampère a um círculo centrado no eixo do cilindro:
Avalie esta expressão para r
Resolva para dentro de para obter:
Passo 3
Avalie esta expressão para r> R:
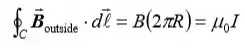
Resolva para dentro de para obter:
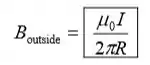
Resposta
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
41- Um solenóide é projetado para produzir um campo magnético igual a 0.0270T em seu centro. Ele possui raio de 1.40c m , comprimento de 40.0c m e o fio conduz uma corrente máxima de 12.0A . ( a ) Qua
Mostre que se a espessura de um toróide for muito pequena comparada com seu raio de curvatura (toróide muito fino), a Eq. 31 -22 para o campo no interior de um toróide se reduz a Eq.31-21 para o campo
Um toróide tendo seção transversal quadrada, com 5,00 cm de lado e um raio interno de 15.0 cm possui 500 espiras e transporta uma corrente de 0.800 A. Qual é o módulo do campo magnético no interior do
Um efeito interessante (e frustrante) ocorre quando tentamos confinar uma coleção de elétrons e íons positivos (um plasma) no campo magnético de um toróide. As partículas que se movem perpendicularmen
Considere um solenoide ideal como um condutor cilíndrico fino, cuja corrente por unidade de comprimento, medida paralelamente ao eixo do cilindro, é λ . Desse modo, mostre que o módulo do campo magnét