Uma casca esférica não condutora, com um raio interno de e um raio externo de , possui uma distribuição de cargas não uniforme. A densidade volumétrica de carga é a carga por unidade de volume, medida em coulombs por metro cúbico. No caso dessa casca, , em que é a distância em metros a partir do centro da casca e . Qual é a carga total da casca?

Fala aí, pessoal! 😎

Nesse problema temos uma casca esférica não condutora, com um raio interno de e um raio externo de , possui uma distribuição de cargas não uniforme. No caso dessa casca, , em que é a distância em metros a partir do centro da casca e . A partir daí queremos descobrir qual é a carga total da casca?

Tem ideia de como fazemos isso? 🤔

Pra começar, vamos fazer uma ilustração:

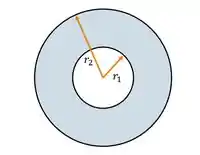
Como a carga não está distribuída de maneira uniformes, vamos ter que usar a densidade superficial, olha só:

Vamos dar uma olhada como fica esse :

Derivando,

Veja só! 🤔