Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 21.Problemas Adicionais - Ex. 58
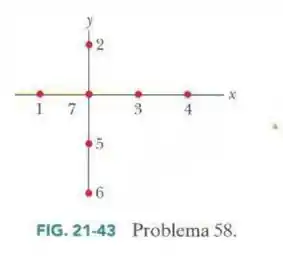
Na Fig. 21-42, seis partículas carregadas cercam a partícula a uma distância de ou , como mostra a figura. As cargas são , , , , , e , com . Qual é o módulo da força eletrostática a que está submetida a partícula ?
Passo 1
Fala aí, galerinha! 😁
Nesse problema temos um sistema com 7 particulas carregadas e nosso objetivo é determinar a força elétrica resultante na partícula que se encontra no centro do sistema.
Tem ideia de como fazemos isso? 🤔
Nesse caso, para determinar a força resultante podemos calcular o somatório da contribuição de cada partícula para a força total.
A força elétrica é dada por
Para varias cargas, podemos manipular essa equação para chegar em
Faremos isso tanto pra vertical quanto pra horizontal, ok?Veja só! 😁
Passo 2
Observando as forças que agem na vertical e na horizontal sobre a carga , temos, sendo as cores das setas correspondentes aos sentidos das forças exercidas pelas cargas de mesma cor:
Vamos fazer várias combinações por aqui ok? No primeiro momento vamos combinar somente com as incógnitas sem olhar pros valores.
Substituindo e temos:
Somando as frações temos a parcela do colchete igual a zero e portanto:
Tranquilo até aqui? 😬
Passo 3
Agora, olhando para as forças atuantes na direção
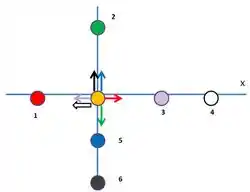
Aqui substituiremos as cargas e .
Eita! e são ambos nulos!
Isso significa que a força eletrostática resultante total, então, é nula.
Bacana, não é? O que achou? Responde Aí! 😉
