Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 10.Problemas - Ex. 98

Centro de percussão. Um bastão de bola de beisebol está em repouso sobre uma superfície horizontal sem atrito. O bastão possui comprimento de 0,900 m, massa de 0,800 kg e seu centro de massa está situado a 0,600 m da extremidade do punho do bastão . O momento de inércia do bastão em relação ao centro de massa é igual a 0,0530 kg . m2. O bastão é golpeado por uma bola de beisebol que se desloca ortogonalmente a ele. O impacto fornece um impulso J =   ∫ t 1 t F d t   em um ponto situado a uma distância x do punho do bastão. Qual deve ser o valor de x para que a extremidade do punho do bastão permaneça em repouso à medida que o bastão se move? (Sugestão: Considere o movimento do centro de massa e a rotação em torno do centro de massa). Ache x de modo que a combinação dos dois movimentos forneça v = 0 para a extremidade do bastão logo após a colisão. O ponto que você localizou denomina-se centro de percussão. Quando uma bola de beisebol colide no centro de percussão, ocorre uma diminuição da força de “picada” que o batedor sente nas mãos.

Passo 1

Eaee, belezinha??? Enunciado gigante ne??? Mas não se desespera não 😉

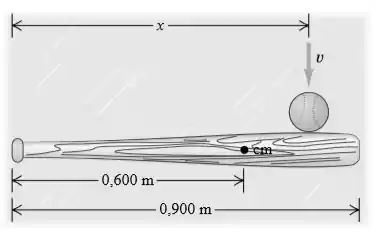
Temos a seguinte figura de um taco de baseball com suas dimensões:

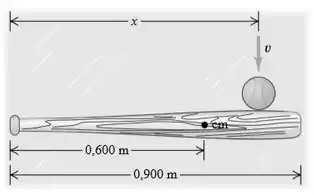
Onde x é a distância que a bola atinge o taco, c m é o centro de massa e v é a velocidade da bola.

Ainda temos como dado a massa do taco ( 0,800   k g ) e o momento de inércia em relação ao centro de massa de 0,0530   k g   .   m 2 .

Queremos calcular o valor de x para que a extremidade do punho do bastão permaneça em repouso à medida que o bastão se move.

Em seguida, devemos calcular x de modo que a combinação dos dois movimentos forneça v = 0 para a extremidade do bastão logo após a colisão.

Passo 2

Faremos o impulso J como sendo:

J = m ∆ v c m

Onde m é a massa do bastão e ∆ v c m é a mudança na velocidade do centro de massa do objeto.

Reorganizando, temos:

∆ v c m =   J m

Enquanto o momento angular ∆ L é:

∆ L =   J ( x - x c m )

∆ L =   ∆ ω I

Onde Δ ω é a variação da velocidade angular e I é o momento de inércia.

Passo 3

Igualando as equações e isolando ∆ω:

∆ ω I =   J ( x - x c m )

∆ ω =   J ( x - x c m ) I

Por fim, teremos que a velocidade final será:

∆ v =   ∆ v c m -   ∆ ω x c m    

∆ v = J m -   J ( x - x c m ) I x c m  

Passo 4

Como a questão pode para admitirmos a velocidade final nula, será possível cancelar “os impulsos” e rearranjando a equação teremos:

0 = J m -   J ( x - x c m ) I x c m

x =   I x c m m +   x c m

Então seguimores (study blogueira), agora não só vamos pôr os valores e finalizar a questão!

Passo 5

Calculando...

x =   I x c m m +   x c m

x =   5,3 . 10 - 2 0,6 0,8 + ( 0,6 )

x = 0,71   m

Resposta

A distância do punho do bastão é igual a 0,71 metros.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um haltere formado por dois discos 1 e 2 iguais, de massa m , unidos por uma barra rígida de massa desprezível e comprimento l = 30c m , repousa sobre uma mesa de ar horizontal. Um terceiro disco 3 de
Uma mesa de coquetel tem um tempo giratório, que é uma tábua circular de raio R e massa M , capaz de girar com atrito desprezível em torno do eixo vertical da mesa. Uma bala de massa m ≪ M e velocidad
Um alçapão quadrado, de lado a e massa M , está levantado verticalmente, em equilíbrio sobre as dobradiças, quando é levado a cair por uma ligeira trepidação. Desprezando o atrito, que a velocidade an
Um disco de massa m 1=80,0g e raio r 1=4,00c m desliza por uma mesa de ar com velocidade v=1,50m / s , como mostrado na Figura P10.53a. Ele faz uma colisão oblíqua com um segundo disco de raio r 2=6,0