Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 11.Problemas - Ex. 16
Um haltere formado por dois discos 1 e 2 iguais, de massa , unidos por uma barra rígida de massa desprezível e comprimento , repousa sobre uma mesa de ar horizontal. Um terceiro disco 3 de mesma massa desloca-se com atrito desprezível e velocidade sobre a mesa, perpendicularmente ao haltere, e colide frontalmente com o disco 2, ficando colado a ele (Fig.). Descreva completamente o movimento subsequente do sistema.
Passo 1
Aqui temos uma colisão entre um haltere formado por dois discos e um terceiro disco que colide com um dos discos do haltere.
Nesse movimento, por se tratar de uma colisão, podemos conservar o momento (O momento sempre se conserva em colisões).
Como teremos tanto o movimento de translação (após a colisão o sistema irá se movimentar em linha reta) quanto de rotação (após a colisão o sistema começará a girar), vamos conservar o momento linear e o momento angular.
Primeiramente, vamos conservar a quantidade de movimento (momento linear). Se liga só:
Assim,
Portanto,
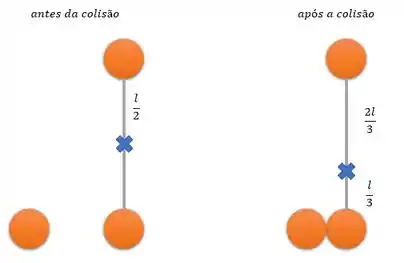
Passo 2
Agora vamos analisar o movimento de rotação. Para isso, vamos conservar o momento angular.
Para o :
Logo,
Para o :
Portanto,
Agora vamos juntar as coisas!
Assim,
Fazendo as coisas:
Passo 3
Agora é só descrever o movimento do sistema.
O centro de massa após a colisão ira se mover com velocidade de na direção de . Além disso, o haltere irá girar em torno do CM com velocidade angular .
Resposta
O centro de massa após a colisão ira se mover com velocidade de na direção de . Além disso, o haltere irá girar em torno do CM com velocidade angular .