Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 11.3 - Ex. 19
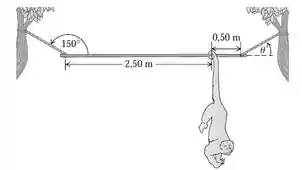
Em um jardim zoológico, uma barra uniforme de m de comprimento e N é mantida em posição horizontal por meio de duas cordas amarradas em suas extremidades (Figura 11.30). A corda da esquerda faz um ângulo de com a barra e a corda da direita faz um ângulo com a horizontal. Um mico de N está pendurado em equilíbrio a m da extremidade direita da barra, olhando atentamente para você. Calcule o módulo da tensão em cada corda e o valor do ângulo . Comece com um diagrama do corpo livre para a barra.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente calcular o módulo da tensão em cada corda e calcular o valor do ângulo que a corda da direita faz com a horizontal. Pra isso, nós sabemos que a bara tem de comprimento e , que a corda da esquerda faz um ângul de com a barra e que um mico de está pendurado na barra a da extremidade direita.
Esboçando tudo isso em um diagrama de corpo livre (DCL), vamos ter:
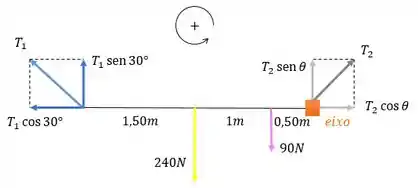
Então, nós vamos ter que encontrar , e . Observe que essas tensões podem ser escritas através das componentes horizontais e verticais, usando o seno ou cosseno do ângulo e que nós convencionamos o sentido anti-horário como positivo.
Assim, vamos aplicar as equações de equilíbrio, fazendo o somatório das forças em cada corda e encontrar as nossas variáveis.
Vamos lá!
Passo 2
Aplicandoo somatório dos somatório dos torques ao eixo na extremidade direita da barra, para o equilíbrio, temos:
Sabemos que torque no sentido anti-horário é positivo, assim, multiplicamos as forças e respectivas distâncias até a caixinha laranja do nosso DCL, que representa a corda da direita, e temos:
Dessa forma, isolando a tensão na equação, temos que:
Passo 3
Agora aplicando equação de equilíbrio das forças na horizontal, , temos que:
Observe que somamos as componentes horizontais das tensões. E temos:
Como e , temos:
E para o equilíbrio na vertical, vamos ter:
Somando as componentes e forças verticais do nosso sistema:
Isso implica que:
Passo 4
Como a gente obteve as tensões em função em do ângulo , agora vamos fazer:
E substituindo e :
Encontramos o ângulo:
Passo 5
Então, podemos calcular a tensão por meio da equação:
Substituindo e isolando , temos:
O macaco está mais perto da corda direita do que da esquerda, então a tensão é maior na corda direita. Os componentes horizontais das tensões devem ser iguais em magnitude e opostos em direção.
Além disso, desde que , a corda à direita deve estar em um ângulo maior acima da horizontal para ter o mesmo componente horizontal que o tensão na outra corda.
Valeu, galera! Até a próxima! 😉
Resposta
e