Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 38.Problemas - Ex. 53

Quando certa superfície fotoelétrica é iluminada com luz de diversos comprimentos de onda, os seguintes potenciais de corte são observados:

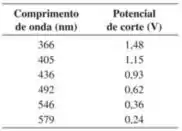
Faça um gráfico colocando o potencial de corte no eixo vertical e a frequência da luz no eixo horizontal. Determine (a) a frequência de corte; (b) o comprimento de onda de corte; (c) a função trabalho do material (em elétrons-volt); (d) o valor da constante de Planck h (supondo que o valor de e seja conhecido).

Passo 1

Então pessoal, essa é uma questão que dá pra resolver de várias formas. Você pode fazer o gráfico à mão ou usar um programa de computador.

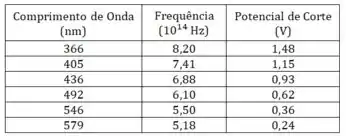
De qualquer forma, vamos explicar como fazer cada um desses itens. O primeiro passo é fazer um gráfico com esse seis pontos que o enunciado deu.

Mas cuidado! Ele pediu a frequência no eixo horizontal, e não o comprimento de onda. Então temos que calcular:

c = λ f         ⇒           f = c λ = 3 × 10 8   m / s λ

Calculando esses valores, vamos encontrar:

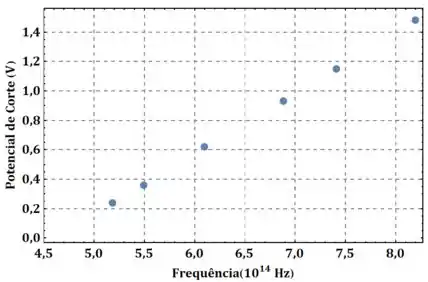
E os pontos devem ficar mais ou menos assim:

Passo 2

Agora temos que traçar uma linha reta ao longo dos pontos no gráfico. Não precisa ser nada muito preciso!

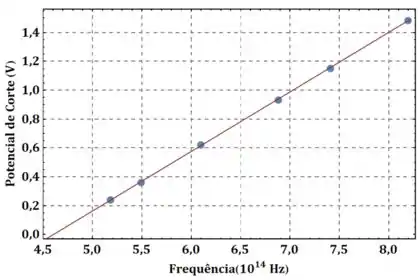
Agora a frequência de corte f 0 é o valor da frequência quando V = 0 . Olhando para o nosso gráfico:

f 0 ≅ 4,55 × 10 14   H z

Beleza. Lembre que é só uma estimativa.

Passo 3

(b) Agora podemos calcular o comprimento de onda associado a essa frequência:

λ = c f

Então:

λ = 3 × 10 8 4,55 × 10 14 = 6,6 × 10 - 7   m

λ = 660   n m

Passo 4

(c) Agora temos que calcular a função trabalho do material. A gente pode fazer isso usando essa fórmula aqui:

Φ = h f 0

E a frequência f 0 que calculamos lá em cima:

Φ = 4,136 × 10 - 15 4,55 × 10 14 = 1,89   e V

Aqui usamos a constante de Planck em elétrons-volt! Porque o enunciado pediu a função trabalho ness unidade.

Passo 5

(d) Agora queremos calcular o valor da constante de Planck.

Bom, a gente sabe que a função que descreve o potencial de corte em função da frequência é essa aqui:

e V 0 = h f - Φ

Então, isolando V 0 :

V 0 = h e f - Φ e

A constante de Planck aparece no coeficiente angular da nossa função! Então vamos calcular o coeficiente angular do nosso gráfico.

É só escolher dois pontos quaisquer (podem ser os da tabela mesmo):

P 1 = 8,20 × 10 14   H z   ,   1,48   V

P 2 = 5,18 × 10 14   H z ,   0,24   V

Então o coeficiente angular é:

α = 1,48 - 0,24 8,20 - 5,18 × 10 14 = 1,24 3,02 × 10 14 V H z

α = 4,106 × 10 - 15   V / H z

E já que o coeficiente angular é α = h / e :

h e = 4,106 × 10 - 15

h = 4,106 × 10 - 15 e

E usando e = 1,60 × 10 - 19   C para a carga elementar:

h = 4,106 × 10 - 15 1,60 × 10 - 19

h = 6,58 × 10 - 34   J ∙ s

Pronto! Chegamos em uma estimativa para a constante de Planck. É bastante próxima do valor verdadeiro:

h = 6,63 × 10 - 34   J ∙ s

Resposta

(a) A frequência de corte é f 0 ≅ 4,55 × 10 14   H z .

(b) O comprimento de onda de corte é λ = 660   n m .

(c) A função trabalho é Φ = 1,89   e V .

(d) Com esses dados podemos estimar h = 6,58 × 10 - 34   J ∙ s .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

um laser usado para soldar retinas descoladas emite luz com comprimento de onda igual a 652 n m através de pulsos que duram 20 n m . A potência média durante cada pulso é igual a 0,6 W . Qual é a ener
O comprimento de onda de corte para o efeito fotoelétrico em uma superfície de tungstênio é 272n m . Calcule a energia cinética máxima dos elétrons emitidos por essa superfície de tungstênio quando el
38.10. Em uma experiencia com efeito fotoelétrico, a energia cinética máxima dos fotoelétrons ejetados é medida em vários comprimentos de onda da luz incidente. A figura 38.35 mostra um gráfico dessa
O comprimento de onda correspondente ao limiar para que ocorra o efeito fotoelétrico no alumínio é de 2 954 Å Å. (a) Qual é a função de trabalho do A l (em e V )? (b) Qual é a energia cinética máxima
38.55. a) O comprimento de onda da luz que incide sobre uma superfície metálica se reduz de λ 1 para λ 2 ( λ 1 e λ 2 são menores do que o comprimento de onda de corte para a superfície). Quando o comp