Complete a dedução da fórmula do espalhamento Compton, Equação (38.23), seguindos os passos indicados da equação (38.24) até a Equação (38.27).

Equação (38.23):

Equação (38.24):

Equação (38.27):

Então vamos lembrar da relação relativística para a energia:

Qual é a energia inicial do sistema? Temos que somar as energias do elétron e do fóton:

O elétron está parado inicialmente , então só vai ter a energia de repouso:

E o fóton incidente tem momento com módulo . Como a sua massa é , a energia do fóton é:

Então:

Beleza, e qual é a energia final do sistema?

Bom, vamos olhar para um instante logo depois da colisão. A energia final do elétron é:

E a energia final do fóton espalhado, que tem momento , é:

Somando essas duas energia finais:

Agora, pelo princípio da conservação de energia:

Para melhorar um pouco, vamos isolar essa raiz quadrada:

E agora elevamos os dois lados ao quadrado:

Já melhorou bastante! Agora vamos aplicar o princípio da conservação de momento.

Olhando para o nosso desenho lá do passo , vamos pensar em como fica a conservação de momento:

No início tínhamos apenas o momento do fóton incidente:

E depois ficamos com os momentos do fóton espalhado e do elétron:

Igualando essas duas expressões:

E podemos representar isso por um desenho usando a rega do paralelogramo:

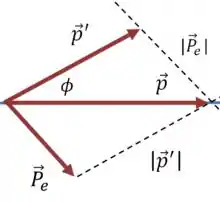
Agora vamos aplicar a lei dos cossenos sobre aquele triângulo de cima.

Os lados com comprimento e são adjacentes ao ângulo , e é o comprimento do lado oposto, então:

Ok agora vamos juntar tudo o que temos.

Usando a conservação de energia, nós chegamos nessa equação aqui:

Temos que “abrir” um pouco mais essa equação, vamos olhar para cada lado separadamente:

Começando por :

Beleza, vamos guardar isso.

Agora vamos olhar para :

Usando a conservação de momento, a gente encontrou essa equação aqui:

Substituindo em :

Agora sim, podemos juntar tudo na equação lá de cima:

Vários termos vão se cancelar agora:

Reorganizando um pouco:

E dividindo tudo por :

E agora dividindo tudo por :

Beleza estamos quase na equação que o enunciado pediu!

Agora só falta fazer um último ajuste. Lembra da relação entre o momento e o comprimento de onda?

Então temos:

Substituindo isso na equação de cima:

Agora é só dividir tudo por :

Pronto! Chegamos na fórmula que o enunciado pediu!