Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 26.3 - Ex. 8
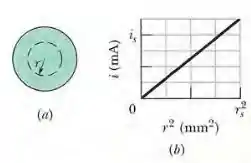
Um certo fio cilíndrico está conduzindo uma corrente. Desenhamos uma circunferência de raio r e centro no eixo do fio (Figura 26-23a) e determinamos a corrente i no interior da circunferência. A Figura 26-23b mostra a corrente i em função de . A escala vertical é definida por e a escala horizontal é definida por (a) A densidade de corrente é uniforme? (b) Caso a resposta do item (a) seja afirmativa, calcule o valor da densidade de corrente.
Passo 1
Aqui temos um fio de raio r pode variar e vemos um gráfico da corrente que passa no fio em função de r, ou seja, quanto maior r maior a corrente que passa pela seção reta delimitada por r
Passo 2
(a) Como a área de um círculo é proporcional a , o eixo horizontal do gráfico da figura do enunciado representa (a menos de um fator constante ) à área do fio. O fato de que o gráfico é uma linha reta indica que a densidade de corrente é constante.
Por isso, a resposta é “sim, a densidade de corrente é uniforme”.
Passo 3
(b) Como, de acordo com o gráfico da do enunciado, a corrente é quando o raio é , temos:
Resposta
(a) sim, a densidade de corrente é uniforme
(b)