Enunciado
Física - Halliday - Vol 3- Ed: 8º - Capítulo 26.3 - Ex. 11
O módulo da densidade de corrente em um fio cilíndrico com de raio é dado por , onde é a distância do centro do fio em metros e . Qual é a corrente que passa em um anel concêntrico com o fio, com de largura, situado a 1,20 mm do centro do fio?
Passo 1
Fala aí! Como vai? 😁
Temos um fio cilíndrico com raio e densidade de corrente não-uniforme em que . Nosso objetivo é determinar a corrente que passa em um anel com de largura e do centro do fio.
Sabemos que a corrente pode ser calculada a partir da fórmula:
E substituindo a densidade de corrente, temos:
No entanto, não queremos a corrente que passa pelo fio, mas sim a corrente que passa por uma porção do fio, que seria um anel.
Saca só! 👀
Passo 2
Sabemos que esse anel é concêntrico com o fio, tem uma largura de e que está a uma distância de do centro do fio. Algo mais ou menos assim:
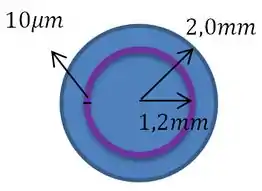
Como só queremos a corrente que passa pelo anel, ou seja, a corrente que passa pelo círculo rosa no desenho acima.
Em um caso normal, nós iríamos agora colocar o raio interno e o externo do anel como sendo os limites de integração e integrar para se calcular a corrente.
Mas podemos usar aqui uma aproximação!
Repara só que a espessura do anel ) é muito menor do que o raio interno e externo do anel.
Sendo assim, usaremos a aproximação:
Onde será o raio médio do anel que é e será a espessura do anel , sendo assim teremos:
Ou se preferir:
E aí! O que achou? Responde Aí! 😎
