Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 27.9 - Ex. 61

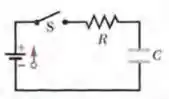
A chave S da Fig. 27-63 é fechada no instante t = 0 , fazendo om que um capacitor inicialmente descarregado de capacitância C = 15,0 μ F comece a se carregar através de um resistor de resiscência R = 20,0 Ω . Em que instante a diferença de potencial entre os terminais do capacitor é igual à diferença de potencial entre os terminais do resistor?

Passo 1

Fala aí, pessoal! 😊

Aqui temos um circuito simples onde temos um capacitor, um resistor e uma fonte e queremos saber o instante de tempo em que a diferença de potencial do capacitor é igual a entre os terminais do resistor.

Tem ideia de como fazemos isso? 🤔

Passo 2

Vamos chamar de V a f e m da fonte. Nesse caso, a condição de que a diferença de potencial

entre os terminais do resistor seja igual à diferença de potencial entre os terminais do capacitor pode ser escrita na forma i R = V c a p , o que, de acordo com as Eqs. 27-34 e 27-35, nos dá

i R e - t R C = V c a p e - t R C = V 1 - e - t R C

Como V c a p = V , temos

i R e - t R C = V e - t R C = V 1 - e - t R C

Simplificando o V :

e - t R C = 1 - e - t R C

e - t R C + e - t R C = 1

2 e - t R C = 1

aplicando l n dos dois lados para eliminar o termo e , temos

- t R C + l n 2 = 0

logo

t = R C l n 2

E como R = 20 Ω e C = 15 μ F ...

t = 0,208 m s

E aí! Sacou? Responde Aí! 😉

Resposta

t = 0,208 m s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No circuito da figura, a chave é ligada em t = 0 , como capacitor descarregado.Ache a energia armazenada em C , após um tempo muito longo.
No circuito da figura, a chave é ligada em t = 0 , como capacitor descarregado. Demonstre que, após um tempo muito longo, metade da energia fornecida pela bateria estará armazenada no capacitor, e a o
No circuito da figura, a chave é ligada em t = 0 , como capacitor descarregado.Ache a energia total fornecida pela bateria, durante esse tempo.
Um capacitor é carregado até um potencial de 12,0 V e a seguir é conectado a um voltímetro com resistência interna igual a 3,40M Ω . Depois de 4,0 s, a leitura do voltímetro indica 3,0 V. Qual é (a) o
Um resistor e um capacitor são conectados em série a uma fonte fem. A constante de tempo para o circuito é de 0,870 s. (a) Um segundo capacitor, identico ao primeiro, é acrescentado em série. Qual é a