Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 10.Problemas Adicionais - Ex. 85
Um ciclista de 70 kg apoia toda a sua massa em cada movimento para baixo do pedal enquanto pedala em uma estrada íngreme. Supondo que o diâmetro da circunferência descrita pelo pedal é 0,40 m, determine o módulo do torque máximo exercido pelo ciclista em relação ao eixo de rotação dos pedais.
Passo 1
Belezera galerinha, antes de começar vamos desenhar o pedal que o ciclista se apoia:
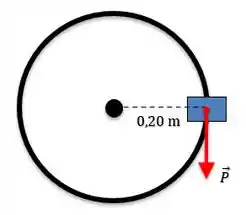
Como o enunciado nos deu um diâmetro , temos que o raio será , além disso, o bloco azul representa o pedal que o cilcista se apoia, enquanto que o circulo grande é a circunferencia descrita pelo pedal.
Passo 2
Belezoca, aqui nós vamos precisar de aplicar a definição de torque, dada como:
Ou da mesma maneira:
Já sabemos através do desenho que:
Agora a força que o ciclista exerce é exatamente a força peso dele, afinal, o enunciado nos diz que o ciclista apoia todo peso do seu corpo sobre o pedal, de forma que:
Passo 3
Agora é o ângulo entre a força peso e o vetor direção que liga o ponto onde a força atua até o eixo de rotação:
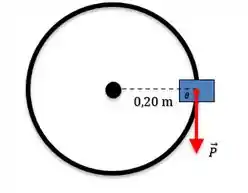
Logo:
Colocando tudo na fórmula do torque, obtemos:
