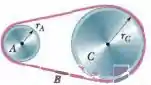
Na Fig. 10-28, urna roda de raio está acoplado por uma correia a uma roda de raio . A velocidade angular da roda é aumentada a partir do repouso a uma taxa constante de . Determine o tempo necessário para que a roda e atinja uma velocidade angular de , supondo que a correia não desliza. (Sugestão: se a correia não desliza, as velocidades lineares das bordas dos discos são iguais.)

Então galera , como a correia não desliza, um ponto da borda da roda tem a mesma aceleração tangencial que um ponto da borda da roda . Isso significa que , onde é a aceleração angular da roda e é a aceleração angular da roda . Assim,

Com a velocidade angular da roda dada por , o tempo para que a roda atinja uma velocidade angular a partir do repouso é