Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 10.9 - Ex. 55
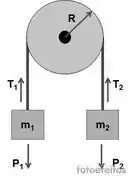
Na figura o bloco 1 tem massa m1 = 460 g , o bloco 2 tem massa 500 g , e a polia ,que está montada em um eixo horizontal com atrito desprezível , tem um raio R = 5 cm.Quando o sistema é liberado a partir do repouso o bloco 2 cai 75 cm em 5 s sem que a borda desilize na borda da polia. Determine:a)Qual é o módulo da aceleração dos blocosb)Qual o valor das tensões T1 e T2.c) Qual é o módulo da aceleração angular da poliad) Qual é o momento de inércia da polia?
Passo 1
Para a aceleração vamos para a função horário do movimento, já que temos altura e tempo de descida.
y = yo + voy + (1/2).a.t² ; sendo que yo =0 e voy =0, logo:
y = (1/2).a.t²
a = 2y / t²
a = 2 . (0,75) / 5²
a = 0,06 m/s²
Passo 2
Com a aceleração escalar do sistema "em mãos", podemos "abraçar" a 2ª Lei de Newton (Fr = m . ay) para determinarmos a tração através da força resultante, para cada bloco. Atentem para dois termos colocados: (i) aceleração escalar e (ii) estamos tratando com a em y (ay).
Passo 3
Assim, teremos para a tração 1:
Fr = m . ay
P - T1 = m1 . a
m1 . g - T1 = m1 . a
T1 = - m1 . a + m1 . g
T1 = 4,54 N
E para a tração 2:
Fr = m . ay
P - T2 = m2 . a
m2 . g - T2 = m2 . a
T2 = - m2 . a + m2 . g
T2 = 4,87 N
Passo 4
Calculando a aceleração angular, em rad/s, temos:
a = α . R
α = a / R
α = 1,20 rad/s²
Passo 5
Para a determinação do momento de inércia vamos recorrer a função do Torque (Ʈ). Onde devemos atentar que o giro pode ocorrer para ambos os lados, logo teremos um torque resultante, já que as massas são distintas. Logo, o torque pode ser dado por:
Ʈr = I . α
Ʈ2 - Ʈ1 = I . α
R . T2 - R . T1 = I . α
R . (T2 - T1) = I . α
I = (R / α) . (T2 - T1)
I = 0,0138 kg.m²
Resposta
a) 6 cm/s^2b) 4,54 N e 4,87 Nc) 1,20 rad/s^2d) 0,0138 kg*m^2