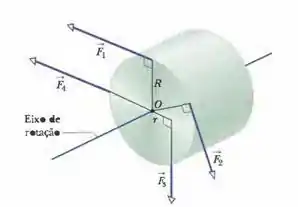
Na figura abaixo, um cilindro com uma massa de 2,0 Kg pode girar em torno do eixo central, que passa pelo ponto O. As forças mostradas têm os seguintes módulos: 1=6,0 N, 2=4,0 N, 3=2,0 N e 4=5,0 N. As distâncias radiais são r=5,0 cm e R=12 cm. Determine (a) o módulo e (b) a orientação da aceleração angular do cilindro. (Durante a rotação, as forças mantêm os mesmos ângulos em relação ao cilindro).

(b)Como a aceleração é positiva, o sentido da aceleração é o sentido anti-horário e o vetor aceleração aponta para fora do papel.

Além disso, o torque foi positivo na letra (a), o que nos diz que o torque resultante está na direção do torque de . Como ele aponta para fora do papel, a aceleração angular será no sentido anti-horário. É só pegar sua mão direita, apontar o polegar na direção do torque resultante (fora do papel) e fechar os outros 4 dedos . Você verá que está fechando no sentido anti-horário.