Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 20.3 - Ex. 43
A figura abaixo mostra uma máquina de Carnot que trabalha entre as temperaturas e e alimenta um reservatório de Carnot que trabalha entre as temperaturas e . Qual é a razão ?
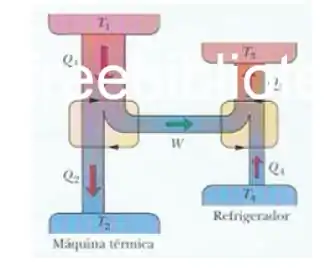
Passo 1
Aqui temos uma máquina térmica de Carnot associada a um refrigerador de Carnot. Primeiro vamos determinar o trabalho fornecido pela máquina. Da fórmula para a eficiência temos:
Assim temos:
Passo 2
Agora vamos calcular através do rendimento, o trabalho consumido pelo refrigerador de Carnot:
Assim temos:
Mas, num refrigerador de Carnot também temos:
E temos também que:
Portanto:
Assim o trabalho do refrigerador em termos de fica:
Passo 3
Daí você me pergunta: e agora? O que eu faço com isso?
Vamos pensar galera! Olha só, a saída da máquina não está ligada a entrada do refrigerador? Então podemos dizer que todo trabalho fornecido pela máquina térmica é consumido pelo refrigerador em termos de trabalho! Assim, podemos igualar as duas expressões para obtida nos dois passos anteriores. Saca só:
Basta agora isolar :
