Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 20.Problemas Adicionais - Ex. 76
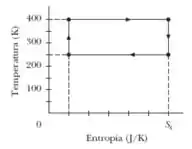
A figura mostra um ciclo de Carnot em um diagrama -. A escala do eixo horizontal é definida por . Determine (a) a transferência líquida de calor por ciclo e (b) o trabalho líquido realizado pelo sistema por ciclo.
Passo 1
Temos um gráfico da temperatura (em ) em função de entropia (em ). Como essas duas grandezas de relacionam com a transferência líquida de calor no sistema?
Mesmo que não lembrasse dessa fórmula, perceba que as unidades dos eixos já dão uma dica, se multiplicarmos uma pela outra, teremos a unidade de energia/calor:
O enunciado diz que , como temos “marcações” no eixo entre e , podemos concluir que cada marcação vale:
Passo 2
(a) Pela nossa equação podemos ver que quando (uma linha vertical no gráfico), o calor transferido também é nulo, então só temos que considerar as duas linhas horizontais.
Na primeira linha:
E na segunda linha:
Então a transferência líquida (resultante) é:
Passo 3
(b) Vamos lembrar da primeira lei da termodinâmica:
Onde é o trabalho realizado pelo sistema. Como estamos lidando com um ciclo fechado, podemos garantir que a variação da energia interna será igual a zero:
Então:
Resposta
(a) A transferência líquida de calor por ciclo é de .
(b) O trabalho realizado por ciclo é .