Em um cilindro, de gas ideal monoatômico incialmente a uma pressão de e à temperatura de se expande até o triplo do seu volume inicial. Calcule o trabalho realizado pelo gas quando a expansão é a) isotérmica; b) adiabática; c) isobárica. d) Usando um diagrama , ilustre cada um desses processos. Em qual deles o trabalho realizado pelo gas possui o maior valor absoluto? E o menor valor absoluto? e) Em qual desses processos o calor trocado possui o maior valor absoluto? E o menor valor absoluto? f) Em qual desses processos a variação de energia interna possui o maior valor absoluto? E o menor valor absoluto?

b) Na expansão adiabática, e a primeira lei da termodinâmica fica:

Usando a equação que relaciona a variação de energia interna com a variação de temperatura:

Podemos substituir na primeira lei, para calcularmos o trabalho:

Como não temos , vamos usar a equação de um processo adiabático para a temperatura:

Como o volume final é o triplo do inicial:

será:

Para um gás monoatômico ideal, e

Substituindo tudo na equação do trabalho de antes:

c) Um processo isobárico ocorre a pressão constante, podemos calcular o trabalho pela equação:

E como o volume final é o triplo do inicial:

Usando a equação dos gases ideais fica o seguinte:

Substituindo os valores:

d) O esboço do gráfico para cada processo é:

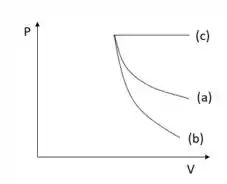
O processo de maior trabalho é o processo isobárico (c), porque a pressão se manteve constante. E o processo de menor trabalho é o adiabático.

e) O processo de maior calor é o isobárico, porque é o de maior valor de calor trocado e o adiabático é o de menor calor já que .

f) o processo isobárico duplicou o valor da temperatura, e como a variação de energia interna está relacionado com ela, ela foi maior nesse processo. O processo de menor é o isotérmico já que a variação de temperatura é zero.