Um cilindro contém oxigênio a uma pressão de 2,0 atm. Seu volume é 4,0 L e a temperatura é 300 K. Suponha que o oxigênio possa ser considerado um gás ideal. O oxigênio é submetido aos seguintes processos:
(i)Aquecido à pressão constante do estado inicial (estado 1) até o estado 2, cuja temperatura é T=450 K.
(ii)Resfriado a volume constante até 250 K (estado 3).
(iii)Comprimido à temperatura constante até um volume de 4,0 L (estado 4).
(iv)Aquecido a volume constante a 300 K, fazendo o sistema retornar ao estado I.
a)Mostre esses quatro processos em um diagrama , fornecendo os valores números de e em cada um dos quatro estados. b) Calcule e em cada um dos quatros processos. c) Ache o trabalho total realizado pelo oxigênio. d) Qual é a eficiência desse dispositivo como máquina térmica? Como se compara essa eficiência com a eficiência de um ciclo de Carnot entre as mesmas temperaturas extremas de 250 K e 450 K?
Passo 1
E aí galera, vamos usar . Aplicaremos as expressões para e que se aplicam a cada tipo de processo.
Para , e .
Passo 2
- Para mostrar esses quatro processos em um diagrama , fornecendo os valores números de e em cada um dos quatro estados, fazemos:
- Bom, agora vamos calcular e em cada um dos quatros processos:
- E o trabalho realiado pelo oxigênio:
- E a eficiência desse dispositivo como máquina térmica:
,,.
.
...
...
Esses processos são mostrados a seguir:
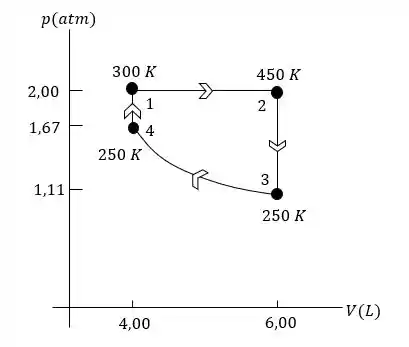
Passo 3
Processo :
Processo 2: .
Processo : e
Processo : .
Passo 4
Passo 5
é muito maior.
Resposta
-

- Processo : ; Processo 2: ; Processo : ; Processo : .