Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 20.2 - Ex. 33
A figura abaixo mostra um ciclo reversível a que é submetido de um gás monoatômico ideal. O volume . O processo é uma expansão adiabática, com e . Determine, para o ciclo completo , a energia fornecida ao gás na forma de calor, a energia liberada na forma de calor e o trabalho líquido realizado pelo gás. Calcule a eficiência do ciclo.
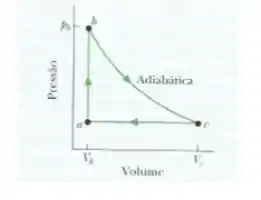
Passo 1
Para determinar o calor absorvido vamos pensar nos dois processos que envolvem a fonte quente: e . O primeiro processo é uma expansão a volume constante, então o calor envolvido é dado por:
O segundo processo é adiabático e processos adibáticos não trocam calor com o meio, então
Assim o calor envolvido será apenas . Para determinar esse valor, precisamos das temperaturas e .
Mas olha que legal! Vamos trocar essa variação de temperatura por algo que fique mais fácil de determinar!
Para uma transformação isocórica, da lei dos gases ideais, temos:
Como temos um mol de gás
Assim o calor será:
Mas daí tu te pergunta, não foi trocar por meia dúzia? Claro que não! e agora só precisamos determinar a pressão em . Mas sabemos que !
Assim da transformação adiabática temos:
Agora sim podemos calcular :
Para um gás monoatômico, , e
Passo 2
A energia liberada na forma de calor vais er dada no processo . Esse processo é uma compressão a pressão constante. E o calor envolvido vai ser:
De forma similar, temos que:
Assim o calor específico à pressão constante fica dado por:
Como , e temos:
Passo 3
O trabalho envolvido é a diferença entre o calor da fonte quente e da fonte fria:
Passo 4
O rendimento de qualquer ciclo é: