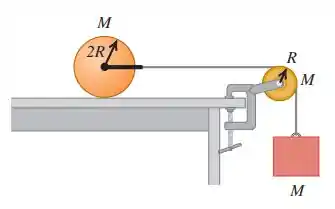
Um cilindro homogêneo de massa e raio está em repouso sobre o topo de uma mesa. Um fio é ligado por meio de um suporte duplo preso às extremidades de um eixo sem atrito passando através do centro do cilindro de modo que o cilindro pode girar em torno do eixo. O fio passa sobre uma polia em forma de disco de massa e raio montada em um eixo sem atrito que passa em seu centro. Um bloco de massa é suspenso na extremidade livre do fio (Figura ). O fio não desliza sobre a superfície da polia, e o cilindro rola sem deslizar sobre o topo da mesa. Calcule o módulo da aceleração do bloco quando o sistema é libertado a partir do repouso.

Nesse problema temos três elementos: um bloco, uma polia e o cilindro.

Usar a conservação de energia vai facilitar muito a nossa vida e simplificar os cálculos, por isso, se o bloco tem velocidade , a polia tem velocidade angular . Como o cilindro está conectado à polia, a sua velocidade angular é também ;)

Então a energia cinética vai ser dada por:

Onde e são as energias cinéticas do cilindro, da polia, cilindro (pela velocidade angular) e do bloco, respectivamente.

Assim, sabendo que a energia cinética é dada por , temos:

Vamos organizar essa expressão:

Show!

Como podemos perceber, o trabalho realizado se dá pela gravidade. Então, a energia cinética expressa:

Onde é a aceleração da gravidade e é a distância de descida é dado por .

Assim, igualando as equações temos

Eliminando o “”, uma vez que a massa é a mesma, em ambos os lados:

E, por fim, isolando a velocidade:

Terminou??? Nãoo!! A gente que a aceleração!

Precisamos lembrar de um detalhe: quando o objeto começa a se deslocar a partir do repouso e de uma altura acima do solo, sua velocidade quando atinge o solo é dada por:

partindo do repouso , temos:

Assim, podemos dizer que a aceleração do bloco é constante:

Por fim, igualando as velocidades, temos:

Prontinho!!