A porta de uma garagem é apoiada sobre um trilho superior (Figura 11.59). As rodas A e B enferrujaram, portanto não giram mais, podendo apenas deslizar ao longo do trilho. O coeficiente de atrito estático é igual a 0,52. A distância entre as rodas é igual a 2,0 m e cada uma delas está a 0,50 m da aresta vertical adjacente da porta. A porta é uniforme e pesa 950 N. Ela é empurrada para a esquerda por uma força horizontal
a) Sabendo que h é igual a 1,60 m, qual deve ser o componente vertical da força exercida sobre cada roda pelo trilho?
b) Calcule o valor máximo de h sem que uma das rodas abandone o trilho.
Passo 1
Vamos aplicar a primeira e segunda condições de equilíbrio para a porta.
Temos a seguinte representação,
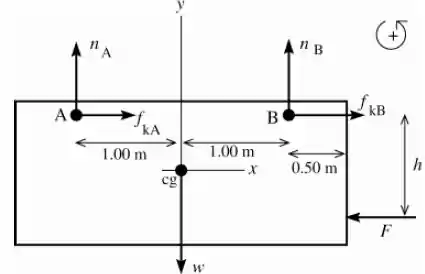
A origem das coordenadas será no centro da porta. As forças envolvidas são , e o normal e forças de atrito exercidas na porta em cada roda.
Passo 2
Agora, vamos relacionar as forças envolvidas no eixo y,
No eixo x,
Como , , então
Mas ainda não acabou... Aplicando a condição de equilíbrio,
Logo,
E, portanto, .
Passo 3
Se h for muito grande, o torque de F fará com que a roda A saia da pista. Quando a oda A apenas começa a levantar fora da pista e ambos vão para zero. Logo,
Com as equações do item (a), temos que
Quando , , temos, .
Logo,
Substituindo os valores...
Resposta
a),
b)