Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 23.4 - Ex. 9
Observa-se experimentalmente que o campo elétrico em uma certa região da atmosfera terrestre aponta verticalmente para baixo. A uma altitude de , o campo tem um módulo de ; a uma altitude de 200 m, o módulo é 100 N/C. Determine a carga em excesso contida em um cubo com 100 m de aresta e faces horizontais a 200 e 300 m de altitude.
Passo 1
Fala meu bom, Yuri aqui e estarei te ajudando a resolver essa atividade.
O problema nos pediu para determinar a carga em excesso contida em um cubo com 100 m de aresta e faces horizontais a 200 e 300 m de altitude, vamos dar uma olhada na situação:
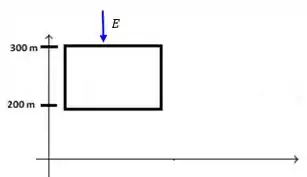
Mas como, faremos isso?
A carga em excesso pode ser achada usando a equação de Gauss:
Passo 2
Aqui nós sabemos que:
Mas não temos nada sobre o fluxo elétrico!
E agora?
Não criemos pânico, podemos achar o fluxo elétrico utilizando sua definição:
Onde é o campo elétrico e é o vetor infinitesimal área que é perpendicular a área.
Passo 3
Aqui pra calcular o fluxo vamos reescrever a equação simplificando um pouco o produto escalar.
Onde é o ângulo entre os vetores e aqui faremos uma análise desse ângulo pra gente saber quais componentes precisamos calcular.
Vamos dar uma olhada nessa figura colocando o vetor campo elétrico e o vetor .
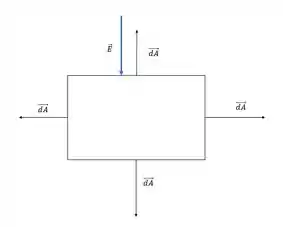
Se o campo está apontando verticalmente para baixo, ele estará paralelo às faces verticais do cubo e perpendicular nas faces horizontais, superior e inferior. E por que isso é importante?
Isso é muito importante porque e para as faces paralelas ao campo, portanto vamos considerar aqui apenas as faces superiores e inferiores.
Repara também que na face superior e na face inferior fazendo com que a combinação nos dê uma parcela negativa em cima e positiva embaixo.
Passo 4
Aqui a gente pode dar uma fugidinha da integral já que a área é constante e o campo e o ângulo não dependem dessa área.
Beleza, chegamos numa expressão pro fluxo, o que fazer agora??
Passo 5
Vamos calcular essa área aí que é constante em cada face.
Substituindo e :
Por fim, colocamos na equação de Gauss:
E é só isso galerinha!!!