Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 91
Um cilindro maciço e uniforme, de madeira, rola descendo um plano inclinado de um ângulo , sem deslizar. O coeficiente de atrito estático é . Determine (a) a aceleração do centro de massa do cilindro, (b) a força de atrito atuando sobre o cilindro e (c) o maior ângulo de inclinação para o qual o cilindro rolará sem deslizar.
Passo 1
Oláaa, querido!
Gente, só temos que pensar o seguinte: só tem três forças atuando, a normal, o peso e o atrito, e só uma delas é capaz de girar o cilindro para a frente, que é o atrito. O diagrama das forças fica assim, ó:
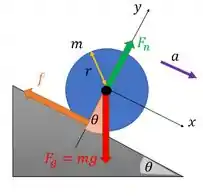
Repara que só o atrito pode fazer esse cilindro girar porque a linha de ação dessa força é a única que não passa pelo centro de massa do cilindro, e assim gera um torque nele.
E como o cilindro não está deslizando, apenas girando, a gente pode dizer que esse atrito é estático.
Bem, depois de perceber essas coisinhas sobre o nosso movimento, bora entrar nos itens, tudo bem?
Passo 2
a) Então, aqui a gente quer a aceleração do centro de massa do cilindro. Para achar essa bonita vamos aplicar a segunda lei de Newton nele.
Já que ele gira, podemos começar aplicando a segunda lei de Newton para a rotação:
O único torque em ação vem da força de atrito. E como ela é perpendicular ao raio, o torque gerado é , assim nossas equação fica:
E como não há deslizamento, podemos relacionar a aceleração angular com a aceleração do centro de massa assim:
Substituindo isso na nossa equação:
O momento de inércia de um cilindro em relação ao seu eixo é . Substituindo isso
Bora isolar porque a gente não conhece ela (já que é força de atrito estático e por isso seu valor depende do problema)
Passo 3
Agora vamos aplicar a segunda lei de Newton para o eixo :
Nessa direção temos a componente da força gravitacional e a força de atrito:
Substituindo a expressão de que a gente achou:
Isolando , quem a gente quer:
Passo 4
b) Queremos . A gente já tem uma expressão para ela. Então vamos substituir nossa expressão de nela.
Voltando na expressão da força de atrito, a gente vai ficar com:
Substituido:
Passo 5
c) Então, cara, ele quer o maior valor de que vai nos dá ainda um movimento só de rotação sem deslizamento. A gente viu que que o mantém a rotação é a força de atrito estática. Então o limite para haver somente rotação é a força de atrito estático máxima:
E quando isso acontece, que estamos na eminência de haver deslizamento no cilindro.
Como queremos mexer com a força de atrito, precisamos achar a força normal. Pra isso vamos olhar pro eixo perpendicular e aplicar a segunda lei de Newton nele:
Então a força de atrito máxima fica:
Passo 6
Maaas, a gente tem uma expressão para a força de atrito:
Igualando essa expressão a do passo anterior:
Isolando quem a gente quer, o :