Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 17.1 - Ex. 76
Um cilindro oco de de massa desprezível repousa de lado em uma mesa horizontal sem atrito. O cilindro é dividido em duas seções iguais por uma membrana não porosa vertical. Uma seção contém nitrogênio e a outra contém oxigênio. A pressão do nitrogênio é duas vezes a do oxigênio. Até que ponto o cilindro se moverá se a membrana quebrar?
Passo 1
O diagrama mostra o cilindro antes da remoção da membrana. A distância que o cilindro se moverá se a membrana romper é a distância entre os locais do centro de massa inicialmente e após a ruptura da membrana. Como os dois gases preencherão o cilindro uniformemente após a ruptura da membrana, a localização do centro de massa após essa ruptura estará no ponto médio do cilindro; isto é, a de cada extremidade do cilindro. Veja o Apêndice C para as massas molares de oxigênio e nitrogênio.
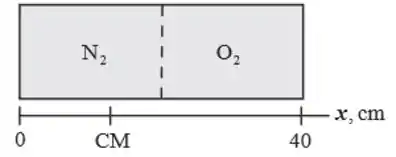
Expressaremos a distância que o cilindro se moverá em termos do movimento do centro de massa quando a membrana for removida:
Lei dos gases ideais para os dois gases:
e
Passo 2
Divindo as duas equações temos que:
Mas como, , temos que:
Expressando a massa de O2 em termos de sua massa molar e do número de moles de oxigênio:
Para o nitrogenio da mesma forma:
Passo 3
Usando a expressão de centro de massa antes da membrana ser removida:
Substituindo os valores numéricos:
Logo, voltando para a primeira equação: