Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 18.Problemas - Ex. 63

Um tubo está conectado e um grande tanque é vedado, e existe ar comprimido entre o topo e a superfície de água. Quando a altura da água h é 3,50 m, a pressão absoluta P do ar comprimido é 4,20 × 10 5 P a . Suponha que o ar sobre a água e expanda com temperatura constante, e considere a pressão atmosférica igual a 1,0 × 10 5 P a . a) Com que velocidade a água sai do tubo quando h = 3,50   m ? b) À medida que a água escoa do tanque, h diminui. Calcule a velocidade para h = 3,0   m e h = 2,0   m . c) Em que altura h o escoamento termina?

Passo 1

Aplicaremos a equação de Bernoulli para relacionar a velocidade do efluxo da água da mangueira com a altura da água no tanque e a pressão do ar acima da água no tanque.

E usaremos a equação do gás ideal para relacionar o volume do ar no tanque à pressão do ar.

Os pontos escolhidos estão descritos na imagem:

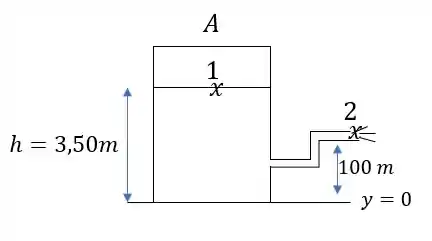
p 1 = 4,20 × 10 5 P a p 2 = p a r = 1,00 × 10 5 P a t a n q u e   g r a n d e   i m p l i c a   v 1 ≈ 0

Passo 2

  1. Assim, aplicando a equação de Bernoulli:

    2. p 1 + ρ g y 1 + 1 2 ρ v 1 2 = p 2 + ρ g y 2 + 1 2 ρ v 2 2

    ⇒   1 2 ρ v 2 2 = p 1 - p 2 + ρ g ( y 1 - y 2 )

    Isso implica que

    v 2 = 2 ρ p 1 - p 2 + 2 g y 1 - y 2

    ⇒ v 2 = 26,2   m / s

    Passo 3

  2. Para h = 3,00   m :

    3. O volume do ar no tanque aumenta e a pressão diminui.

    p V = n R T = c o n s t a n t e

    então p V = p 0 V 0   ( p 0 é a pressão para h = 3,50   m e e p é a pressão para h = 3,00   m )

    p 4,00 m - h A = p 0 4,00 m - h 0 A

    ⇒ p = p 0 4,00 m - h 0 4,00 m - h = 4,20 × 10 5 P a 4,00 m - 3,50 m 4,00 m - 3,00 m = 2,10 × 10 5   P a

    Passo 4

    Repetindo o cálculo da parte (a), mas agora p 1 = 2,10 × 10   P a e y 1 = 3,00   m :

    v 2 = 2 ρ p 1 - p 2 + 2 g y 1 - y 2

    ⇒ v 2 = 1 6 , 1   m / s

    Passo 5

    Para h = 2 , 00   m :

    p = p 0 4,00 m - h 0 4,00 m - h = 4,20 × 10 5 P a 4,00 m - 3,50 m 4,00 m - 2 , 00 m = 1,05 × 10 5   P a

    v 2 = 2 ρ p 1 - p 2 + 2 g y 1 - y 2

    ⇒ v 2 = 5,44 m / s

    Passo 6

  3. Quando v 2 = 0 significa que 2 ρ p 1 - p 2 + 2 g y 1 - y 2 = 0 .

⇒ p 1 - p 2 = - ρ g ( y 1 - y 2 )

⇒ y 1 - y 2 = h - 1,00 m

p = p 0 4,00 m - h 0 4,00 m - h = 4,20 × 10 5 P a 4,00 m - 3,50 m 4,00 m - h

Esse é o p 1 , então

4,20 × 10 5 P a   0,50 m 4,00 m - h - 1,00 × 10 5 P a = 9,8 m / s 2 ⋅ 1000 k g / m 3 ⋅ 1,00 m - h )

210 4,00 - h - 100 = 9,80 - 9,80 h , com h em metros

210 = 4,00 - h 109,8 - 9,80 h

9,80 h 2 - 149 h + 229,2 = 0

E

h 2 - 15,20 h + 23,39 = 0

Pela formula quadrática:

h = 1 2 15,20 ± 15,20 2 - 4 23,29 = 7,60 ± 5,86 m

h deve ser menor que 4,00   m , portanto, o único valor aceitável é h = 7,60   m - 5,86   m = 1,74   m .

Resposta

  1. v 2 = 26,2   m / s
  2. Para h = 2,00 m : v 2 = 5,44 m / s

    3. Para h = 3,00 m : v 2 = 16,1   m / s

  3. h = 1,74   m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

18.5. a) Use a lei do gás ideal para estimar o número de moléculas de ar no seu laboratório de física, supondo que todo o ar seja composto por N 2 . B) Calcule a densidade das partículas no laboratóri
Um recipiente de 1,20 mol de gás nitrogênio (28,0 g/mol a 25° C é deixado no satélite de Júpiter após o final de uma futura missão espacial. A atmosfera de Europa é desprezível, e a aceleração da grav
Na equação do gás ideal, o numero de moles por volume n / V é simplesmente igual a P / R T . Na equação de van der Waals, obter n / V em termos de pressão P e da temperatura T não é tão simples. a) Mo
Durante uma hora, uma pessoa comum em repouso inala 0,50 L de oxigênio a cada respiração a uma pressão de 1,0 atm e uma temperatura de 20 ° C . O gás aspirado possui 20 % do oxigênio. a) Quantas moléc
Um tanque cilíndrico vertical contém 1,80 mol de um gás ideal a uma pressão de 1,00 atmosfera a 20° C . A parte redonda do tanque tem um raio de 10,0 cm, e o gás está sustentando um pistão que poe se