Um cilindro oco tem massa , raio externo e raio interno . Use integração para mostrar que o momento de inércia em relação a seu eixo é dado por . Dica: reveja a seção 9-3, onde é calculado o momento de inércia de um cilindro maciço por integração direta.

Primeiro a gente precisa decidir quem vai ser o elemento. A gente pode pensar em um anel bem fino, de expessura (essa é a notação para um pedaço bem pequeno de , essa é a expessura do anel, bem fina), altura e raio :

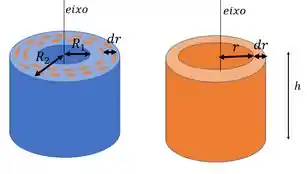
O que a gente faz normalmente para reescrever é usar a massa espefícifica do sólido. Aquela dada pela fórmulinha:

Aí, se temos uma massa , ela pode ser escrita como

Onde é o volume do elemento.

Então a integral fica:

Aí temos que escrever em função de e . Podemos usar derivadas. Como? Um cilindro de raio e altura tem volume

Para achar esse , a gente deriva esse cara em relação a , usando a regrinha de derivar polinômios:

E isola :

Achamos! Aí é substituir na integral:

Para integrar, só faltar saber os extremos de integração. é a distância do eixo até o sólido. Então o menor valor de que encontra nosso sólido é (raio interno do cilindro) e o maior valor de é (raio externo do cilindro). Então nós teremos como extremos de integração:

Substituindo isso na nossa integral:

Tirando o que é não está em função de de dentro dela:

Calculando pela regrinha de polinômios:

Esse é um produto notável do tipo . Então vamos reescrever:

Agora a gente deixa isso com a cara da expressão do enunciado. Como?

A gente pode escrever a massa do cilindro todo como

E o volume do cilindro oco é calculado como:

Então a massa fica

Isolando :

Substituindo isso na expressão do :