Enunciado
Física - Hibbeler - Estática- Ed: 14º - Capítulo 10.Problemas - Ex. 37
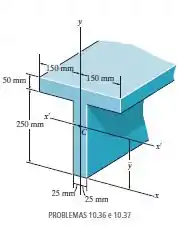
Determine , que localiza o eixo centroidal da área da seção transversal da viga , e depois calcule o momento de inércia em relação ao eixo .
Passo 1
Oi tudo bem? Vamos resolver este exercício.
Temos que determinar o valor de que é o centroide com relação ao eixo e que localiza o eixo e depois calcular o momento de inércia da viga com relação a esse eixo.
Como resolver problemas de momento de inércia de um elemento com geometria não simétrica?
Bem... Um modo bem prático é dividir o elemento em partes, calcular o momento de inércia de cada parte com relação ao eixo e somar os resultados.
Aqui, podemos dividir a área da seção transversal do elemento da seguinte maneira:
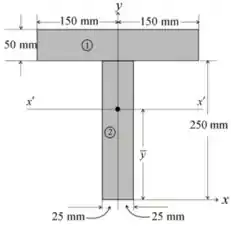
É importante separar as partes, sabendo os seus respectivos centroides.
Vamos aos cálculos!
Passo 2
Para o cálculo de , temos que:
Ficou confuso com a fórmula? Vem comigo então!
Esta equação indica que o valor de é dado pela soma do produto entre o centroide e a área de cada elemento dividido pela soma das áreas de cada elemento.
Como dividimos a viga em dois elementos, temos que:
Agora é só substituir os valores e calcular:
Passo 3
Agora vamos calcular o valor do momento de inércia da viga com relação ao eixo .
Sabendo que para elementos retangulares, temos que:
Onde representa o comprimento da base do elemento, representa o comprimento da altura do elemento, representa o valor da área do elemento e a distância do centroide do elemento até o eixo a ser medido.
Para o elemento , temos que:
Para o elemento , temos que:
Portanto: