Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 22.1 - Ex. 50
Um cilindro sólido não condutor infinitamente longo de raio tem uma massa específica volumétrico uniforme de . Mostre que o campo elétrico é dado pelas seguintes expressões: para e para onde é a distância ao eixo do cilindro.
Passo 1
Fala galera. Esse exercício trata sobre um cilindro não condutor que está uniformemente carregado. Sendo assim, podemos utilizar a lei de Gauss e aproveitar a simetria cilíndrica do problema.
Passo 2
- Para pontos no interior, temos que
- Para pontos externos, temos
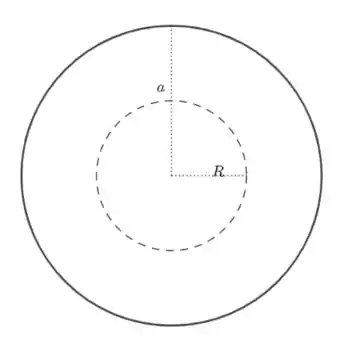
Vamos calcular a carga interna:
sendo o comprimento do cilindro. Logo, temos que
Passo 3
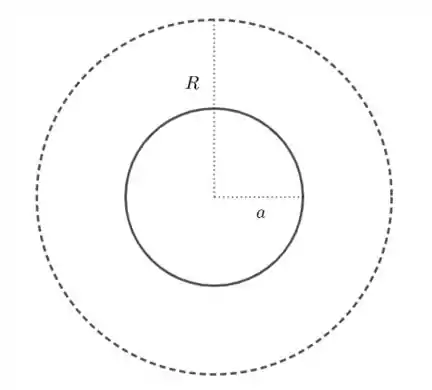
Aqui a carga interna é a própria carga do cilindro:
Logo, temos
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Quando uma esfera metálica, eletricamente neutra, de raio a , está imersa num campo elétrico uniforme de módulo E , encontra-se que a densidade superficial de carga induzida sobre a esfera é σ = 3 ϵ 0
(a) Para a situação do Problema 60, qual é a força eletrostática entre a carga + q e a carga induzida sobre o plano condutor? Ela é atrativa ou repulsiva? (b) Que carga, colocada na posição simétrica
Um átomo de hidrogénio pode ser considerado possuidor de um próton central de carga (puntiforme) positiva e e um elétron de carga negativa - e , distribuída ao redor do próton de acordo com a densidad
A F i g .25 - 41 a mostra um cilindro fino, maciço, carregado, e uma casca cilíndrica coaxial, também carregada. Os dois objetos são feitos de material isolante e possuem uma densidade superficial de
Uma carga de densidade linear uniforme 2,0n C / m está distribuída ao longo de uma barra longa, fina, isolante. A barra está envolvida por uma casca longa, cilíndrica, coaxial, condutora (raio interno