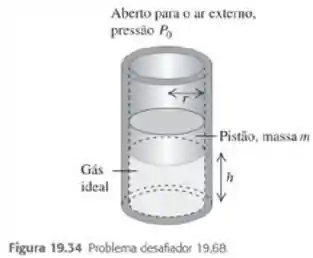
Um cilindro vertical de raio contem uma quantidade de gas ideal e possui um pistao ajudstado de massa que pode se mover livremente (Figura 19.34). Não existe átrio tenre o pistao e as paredes do cilindro e todo o clindrio é colocado em um banho sob temperatura constante. A pressão do ar externo é . No equilibro, o pistao esta a uma altura acima da base do cilindro. a) Calcule a pressão absoluta do gas preso abaixo do pistao na posição de equilíbrio. b) O pistao é puxado para cima e uma distancia pequena, e a seguir é libertado. Calcule a força resultante que atua sobre o pistao quando ele está a uma distancia igual a acima da base do cilindro, onde é muito menor do que . c) Depois que o psitao é puxado para cima e libertado, ele oscila para cima e para baixo. Calcule a frequência dessas pequenas oscilações. Se o deslocamento não for pequeno, o movimento continua sendo harmônico simples? Como você pode ter certeza disso?

b) Primeiro o pistão é levantado, vamos precisar calcular a força para levantar o pistão um pouco, essa força é a própria força peso do pistão mais a força da pressão atmosférica. Ao soltarmos ele, a força muda de sentido e passa a ser exercida de cima para baixo sobre o pistão.

A força que exercemos é:

Que é a força necessária para levantar o pistão. E será a força para baixo sobre o pistão no momento que ele for largado.

Para a força exercida pelo gás sobre o pistão, de baixo para cima, podemos usar a equação do gás ideal para relacionar a situação final, que é da altura do pistão com a inicial de altura :

Como as temperaturas são iguais nos dois estados do sistema, podemos cortar:

Escrevendo o volume em função da área e da altura:

Substituindo a pressão inicial que encontramos na letra (a):

Multiplicando os dois lados pela área da seção reta:

Como o enunciado diz que , o último termo da equação pode ser escrito como:

E isso é aproximadamente:

A equação da força exercida pelo gás fica:

Fazendo a soma das duas e considerando que o sentido positivo é para cima, deixando a primeira equação negativa, já que é a força do pistão assim que foi abandonado:

Substituindo a área pela área do cilindro:

c) Para um movimento harmônico simples, podemos relacionar a frequência das oscilações com uma constante de força:

Podemos considerar que o sistema se comporta como um sistema massa-mola, e a força resultante pode ser escrita como:

Sendo o deslocamento pequeno em torno da posição de equilíbrio que era .

vai ser:

E a frequência:

Se esse deslocamento fosse suficientemente grande ao levantarmos o pistão, a força da atmosfera e a força peso sobre o pistão seriam praticamente uma constante, a força do gás sobre o pistão seria bem mais baixa, e a força da pressão atmosférica muito maior, já que o gás está rarefeito no interior do cilindro, fazendo com que o movimento não produza pequenas oscilações, e por isso, não é harmônico simples.