Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 28.1 - Ex. 68
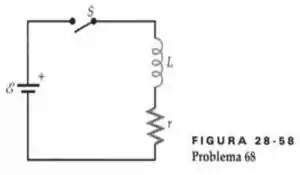
Um circuito consiste em uma bobina que tem auto-indutância igual a 5,00 mH e a resistência interna igual a , uma bateria ideal de 12,0 V e uma chave aberta – todos conectados em série (Figura 28-58). Em t = 0, a chave é fechada. Determine o instante em que a taxa na qual a energia é dissipada na bobina é igual à taxa na qual a energia magnética é armazenada na bobina.
Passo 1
Meus grandes gênios!
Assumindo que, inicialmente, a corrente será igual a 0, a equação que fornecerá o valor da corrente em função do tempo será:
Onde:
Tendo em mãos essa relação, poderemos encontrar o instante em que a taxa na qual a energia é dissipada na bobina é igual à taxa na qual a energia magnética é armazenada na bobina ao encontrar a fórmula que relaciona ao igualar as taxas.
Passo 2
Vamos encontrar a equação do armazenamento da energia magnética na bobina:
E a equação que fornece a relação da energia dissipada na bobina:
Igualando:
Teremos:
Passo 3
Porém, quem será
Sendo:
Por fim, só precisamos igualar as duas relações:
Fazendo os devidos cortes:
Aplicando em ambos os lados:
Substituindo os valores fornecidos pela questão: