Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 25.1 - Ex. 97

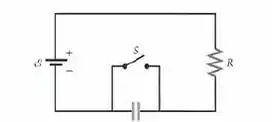
No circuito da Figura abaixo, a fem é igual a 50.0   V e a capacitância é igual a 2.00   μ F . A chave S é aberta depois de permanecer fechada por um longo tempo, e 4.00 s depois, a queda de tensão no resistor é 20.0   V . Determine a resistência do resistor.

Passo 1

FALA GALERA, voltamos para mais uma questão envolvendo corrente elétrica em circuitos de corrente direta (nomezin grande). Podemos achar a resistência do circuito através da razão entre o tempo constante e a capacitância; Expressaremos o tempo constante como uma função de tempo com os termos V 0 e V ( t ) . Utilizaremos as seguintes fórmulas:

R = τ C (1)

V t =   I t R (2)

I t =   I 0   e - t / τ (3)

DITO ISTO, VAMOS POR A MÃO NA MASSA!

Passo 2

Primeiramente, vamos aplicar a equação 3 na equação 2:

V t =   I t R

V t = I 0   e - t / τ   R  

V t = ( I 0   R ) e - t / τ

V t = V 0   e - t / τ  

L n ( V t ) = L n ( V 0   e - t / τ )  

L n V t = L n e - t τ + L n ( V 0 )

L n V t = - t τ + L n ( V 0 )

L n V t - L n ( V 0 ) = - t τ

L n V t V 0 = - t τ

τ = - t L n V t V 0

Agora, substituiremos o resultado do tempo constante na equação 1:

R = τ C

R = - t L n V t V 0 C

R = - t C   L n V t V 0

Encontrado a equação que representa a resistência, basta substituir as variáveis pelos dados estabelecidos na questão:

R = - t C   L n V t V 0

R = - 4.00   s ( 2.00   μ F )   L n 20.0   V 50.0   V

R = 2.18   M Ω

AÍ ESTÁ, tudo feito com sucesso!

É TUDO POR HOJE, bons estudos ;)

Obs: Vai beber água que ta na hora, obrigado, de nada.

Resposta

R = 2.18   M Ω

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um capacitor está descarregando através de um resistor. Se levar um tempo T para que a carga no capacitor se reduza à metade do seu valor inicial, quanto tempo (em termos de T ) levará para que a ener
Mostre que a Equação d Q d t = ℇ C - Q R C ℇ pode ser reescrita como d Q ℇ C - Q = d t R C ℇ . Integre esta equação para derivar a solução dada pela Equação Q f ( 1 - e - t / R C ) .
A chave S mostrada na figura abaixo é fechada depois de ter permanecida aberta por um longo tempo. (a) Qual é o valor inicial da corrente na bateria logo aos a chave S ter sido fechada? (b) Qual é a c
Uma carga constante de 1,00m C está na placa carregada positivamente do capacitor de 5,00μ F mostrado na figura abaixo. Determine (a) a corrente na bateria e (b) as resistências R 1 ,R 2 , R 3 .
Em t = 0 o interruptor na Figura abaixo é girado para o contato b depois de ter estado no contato a por um longo tempo. (a) Determine a energia armazenada no capacitor depois de o interruptor ter sido