Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 25.1 - Ex. 96

Em t = 0 o interruptor na Figura abaixo é girado para o contato b depois de ter estado no contato a por um longo tempo. (a) Determine a energia armazenada no capacitor depois de o interruptor ter sido girado para longe de a. (b) Determine a energia armazenada no capacitor como função do tempo. (c) Esboce um gráfico da energia armazenada no capacitor versus o tempo t.

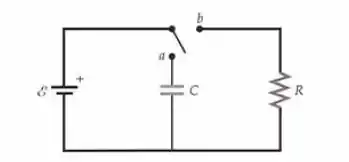
Passo 1

EAE GALERA, LET’S GO, calma, calma, antes de resolvermos a questão, devo informar que os dados que serão utilizados se encontram na questão anterior (95), porque a que responderemos está relacionada com ela, blz? Então vamos nessa!

Bem, para resolvermos essa questão usaremos duas equações, uma para calcular a energia armazenada no capacitor e a outra para expressar a energia do capacitor como uma função de tempo, eis aqui os doces:

U 0 = 1 2   C   ℇ 2 (1)

U ( t ) = 1 2   C   ( V c ( t ) ) 2 (2)

Lembrando que V c t = V 0   e - t / τ ; COM ISSO ESTABELECIDO, vamos resolver essa questão, sigam-me os bons!

Passo 2

Para resolvermos a alternativa (a), usaremos a equação 1 e os dados estabelecidos na questão 95:

U 0 = 1 2   C   ℇ 2

U 0 = 1 2   ( 600 μ F )   ( 100   V ) 2

U 0 = 30.0   m J

Para a alternativa (b) usaremos a equação 2:

U ( t ) = 1 2   C   ( V c ( t ) ) 2

U ( t ) = 1 2   C   ( V 0   e - t / τ ) 2

U ( t ) = 1 2   C   ( ℇ   e - t / τ ) 2

U t = 1 2   C   ℇ 2   e - 2 t / τ

U t = U 0   e - 2 t / τ

Para a alternativa (c) utilizaremos o resultado obtido na alternativa (b) para fazer um esboço do gráfico, ele ficou assim ó:

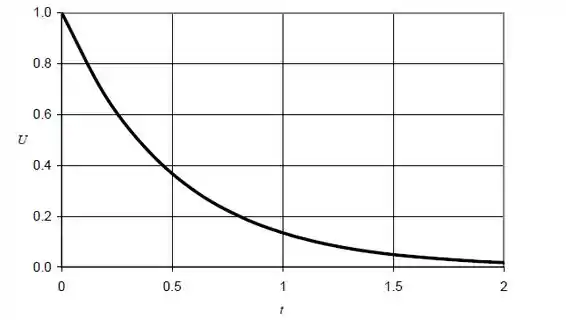
PRONTINHO! Até a próxima galera e bons estudos!

Resposta

a) U 0 = 30.0   m J

b) U t = U 0   e - 2 t / τ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No circuito da figura, a chave é ligada para t = 0 , com o capacitor descarregado. Calcule a voltagem V t através do capacitor após um tempo t .
50- O aquecedor de um secador elétrico possui uma potência máxima especificada igual a 4.1k W para uma fonte de 240V . ( a ) Qual é a corrente que passa no elemento aquecedor? Um fio com calibre 12 po
40- Um capacitor de 12.4μ F é conectado através de um resistor de 0.895M Ω a uma diferença de potencial constante de 60.0V . ( a ) Calcule a carga do capacitor nos seguintes instantes depois que a con
(Veja o problema 26.73). (a) Qual é o potencial do ponto a ao ponto b na Figura 26.76 quando a chave S está aberta? (b) Qual dos pontos, a ou b , possui o potencial mais elevado? (c) Qual é o potencia
Um capacitor inicialmente descarregado é conectado em série a um resistor e uma fonte de fem ε = 110V , que possui resistência interna desprezível. Imediatamente após a ligação do circuito, a corrente