Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 25.1 - Ex. 116

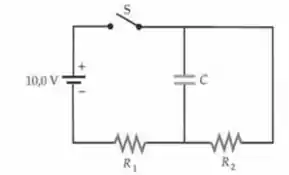
No circuito mostrado na Figura 25-78, R 1 = 2,00   M Ω , R 2 = 5,00   M Ω , e C = 1,00   μ F . O capacitor está inicialmente sem carga em ambas as placas. Em t= 0, a chave S é fechada e, em t= 2,00 s, a chave S é aberta.

a) Esboce um gráfico da tensão em C e da corrente em R 2 entre t= 0 e t= 10,0 s.

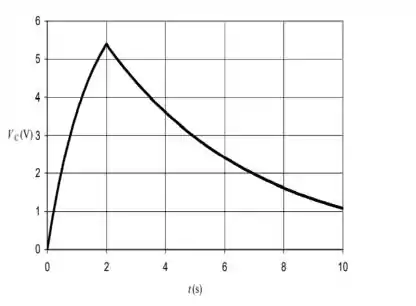
b) Determine a tensão no capacitor em t= 2,00 s e em t= 8,00 s.

Passo 1

a)

Meus queridos!

Essa questão é simples.

Vamos usar a seguinte equação e vamos chama-la de Eq.1 :

I 1 = I 2 + I 3 ; E q . 1

Logo em seguida, sabemos que

ε - Q C - R 1 I 1 = 0 ; E q . 2

Q C - R 2 I 2 = 0 ; E q . 3

Vamos derivar as equações 2 e 3 em função do tempo!

d d t ε - Q C - R 1 I 1 = 0

R 1 d I 1 d t = - 1 C d Q d t

R 1 d I 1 d t = - 1 C I 3

d d t Q C - R 2 I 2 = 0

R 2 d I 2 d t = 1 C d Q d t

R 2 d I 2 d t = 1 C I 3

Sabendo que:

I 3 = ( R 2 C ) d I 2 d t

Vamos aplicar na equação 1:

I 1 - I 2 = ( R 2 C ) d I 2 d t

d I 2 d t = I 1 - I 2 R 2 C

Lembrem-se:

ε - Q C - R 1 I 1 = 0

I 1 = ε - Q C R 1

I 1 = ε - R 2 I 2 R 1

Por fim (finalmente, né?) vamos substituir a relação de I 1 encontrada na equação diferencial:

d I 2 d t = 1 R 2 C ε - R 2 I 2 R 1 - I 2

Isolando:

d I 2 d t = ε R 1 R 2 C - R 1 + R 2 R 1 R 2 C I 2

Passo 2

Para encontrar a equação I 2 ( t ) vamos ter que resolver a EDO:

I 2 t = a + b e - t τ

Logo:

d I 2 d t = d d t a + b e - t τ = - b τ e - t τ

Sendo:

d I 2 d t = ε R 1 R 2 C - R 1 + R 2 R 1 R 2 C I 2

Vamos substituir:

- b τ e - t τ = ε R 1 R 2 C - R 1 + R 2 R 1 R 2 C ∙ a + b e - t τ

Por comparação encontramos que:

τ = R 1 R 2 C R 1 + R 2

E que:

a = ε R 1 + R 2

Tendo:

I 2 0 = 0 = a + b

b = - a = - ε R 1 + R 2

Ora ora, se:

I 2 t = a + b e - t τ

Então:

I 2 t = ε R 1 + R 2 - ε R 1 + R 2 e - t τ

Portanto:

I 2 t = ε R 1 + R 2 1 - e - t τ

Com:

τ = R 1 R 2 C R 1 + R 2

Substituindo os valores fornecidos pela questão, encontraremos:

τ = 1,43   s

I 2 t = 1.429 ∙ 1 - e - t 1.43

Como C e R 2 estão em paralelo, eles tem DDP dada por:

V C t = V 2 t = I 2 t R 2 = 1.429 ∙ 5.00 ∙ 1 - e - t 1.4 29 = 7.143 ∙ 1 - e - t 1.4 29

Com isso:

V C 2 = 7.143 ∙ 1 - e - 2.00 1.429

V C 2 = 5.381   V

O gráfico é dado por:

Passo 3

b)

Como determinamos anteriormente:

V C t = V 2 t = I 2 t R 2 = 1.429 ∙ 5.00 ∙ 1 - e - t 1.429 = 7.143 ∙ 1 - e - t 1.429

Com isso:

V C 2 = 7.143 ∙ 1 - e - 2.00 1.429

V C 2 = 5.381   V = 5.38   V

Agora precisamos calcular o novo valor da constante:

τ ' = R 2 C = 5.00 1.00 = 5.00   s

Sabendo que:

V C t = V C 0 e t - 2.00 5.00

Precisamos calcular nos 8 segundos restantes para completar 10 segundos!

V C 8 = 5.381 e - 6.00 5.00 = 1.62   V

Resposta

a )

b )   V C 2 = 5.38   V   e   V C 8 = 1.62   V  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A Fig. 27-67 mostra dois circuitos com um capacitar carregado que pode ser descarregado através de um resistor quando uma chave é fechada. Na Fig. 27-67a, R 1 = 20,0 Ω e C 1 = 5,00 μ F . Na Fig. 27-67
A chave S da Fig. 27-63 é fechada no instante t = 0 , fazendo om que um capacitor inicialmente descarregado de capacitância C = 15,0 μ F comece a se carregar através de um resistor de resiscência R =
Que múltiplo da constante de tempo τ é o tempo necessário para que um capacitor inicialmente descarregado seja carregado com 99,0% da carga final em um circuito RC série?
Um capacitor com uma carga inicial q 0 é descarregado carregado através de um resistor. Que múltiplo da constante de tempo τ é o tempo necessário para que o capacitor descarregue (a) um terço da carga
Em um circuito RC série, ε = 12,0 V , R = 1,40 M Ω e C = 1,80 μ F . (a) Calcule a constante de tempo. (b) Determine a carga máxima que o capacitor pode receber ao ser carregado. (c) Qual é o tempo nec