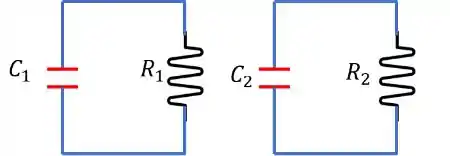
A Fig. 27-67 mostra dois circuitos com um capacitar carregado que pode ser descarregado através de um resistor quando uma chave é fechada. Na Fig. 27-67a, R 1 = 20,0 Ω e C 1 = 5,00 μ F . Na Fig. 27-67b, R 2 = 10,0 Ω e C 2 = 8,00 μ F . A razão entre as cargas iniciais dos dois capacitares é q 02 / q 01 = 1,50 . No instante t = 0 , as duas chaves são fechadas. Em que instante os dois capacitores possuem a mesma carga?

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 27.9 - Ex. 68

A Fig. 27-67 mostra dois circuitos com um capacitar carregado que pode ser descarregado através de um resistor quando uma chave é fechada. Na Fig. 27-67a, e . Na Fig. 27-67b, e . A razão entre as cargas iniciais dos dois capacitares é . No instante , as duas chaves são fechadas. Em que instante os dois capacitores possuem a mesma carga?

Passo 1

Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa atividade. Nesta situação queremos saber em qual momento deste circuito os dois capacitores irão possuir a mesma carga.

Passo 2

Vamos escrever a equação para a carga dos dois capacitores:

Onde e são as cargas iniciais e é a constante de tempo.

Passo 3

Agora, quando os dois capacitores possuem a mesma carga, temos:

Podemos calcular a constante do tempo:

Portanto:

Substituindo os valores:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O circuito da Fig. 27-75 mostra um capacitor, duas fontes ideais, dois resistores e uma chave S. Inicialmente, a chave S permaneceu aberta por um longo tempo. Se a chave é fechada e permanece nesta po

A Fig. 27-63 mostra uma fonte ideal de força eletromotriz ε = 12 V , um resistor de resistência R = 4,0 Ω e um capacitor descarregado de capacitância C = 4,0 μ F . Se a chave S é fechada, qual é a cor

Na Fig. 27-66, a força eletromotriz da fonte ideal é ε = 30 V , as resistências são R 1 = 20 k Ω e R 2 = 10 k Ω e o capacitor está descarregado. Quando a chave é fechada no instante t = 0, determine a

No circuito da figura, a chave é ligada em t = 0 , como capacitor descarregado.Obtenha a energia total dissipada no resistor durante esse tempo. Mostre que a metade da energia fornecida estará armazen

No circuito da figura, a chave é ligada em t = 0 , como capacitor descarregado.Ache a corrente I em função do tempo.