Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 25.1 - Ex. 105
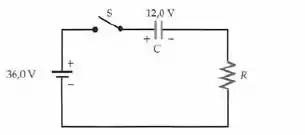
No circuito mostrado na figura abaixo, o capacitor tem capacitância de e o resistor tem resistência de . Antes de a chave ser fechada, a queda de potencial no capacitor é , como mostrado. A chave S é fechada em . (a) Qual é a corrente imediatamente depois de a chave S ter sido fechada? (b) Em que instante t a tensão no capacitor é ?
Passo 1
EAE GALERA, vamos para mais uma envolvendo analise de circuitos! É aquela boa e velha aplicação da Segunda Lei de Kirchhoff’s, para a alternativa (a), basta usar a queridinha segunda lei no circuito logo depois que a chave é fechada, já para a alternativa (b), nos resta aplicar mais uma vez a segunda lei para encontrar a tensão aplicada no resistor quando a tensão no capacitor for igual a , com isso usaremos a expressão para a corrente que passa no resistor e resolveremos para t. DITO ISTO, LET’S GO!
Passo 2
Aplicando a Segunda Lei de Kirchhoff’s imediatamente após a chave do circuito for fechada:
RÁPIDO, FÁCIL, LIGEIRO, com isso aniquilamos a alternativa (a). VAMOS PARA A (B).
Passo 3
Para a resolução da (b) aplicaremos a Segunda Lei de Kirchhoff’s quando a tensão no capacitor for igual a e resolveremos para (tensão no resistor):
Agora expressando a correndo em função de e :
Sabendo que , podemos substituir isso na equação:
PRONTINHO, Detonamos mais uma (toca aqui!)
Resposta
a)
b)