Enunciado
Física - Halliday - Vol 3- Ed: 4º - Capítulo 36.Exercícios e Problemas - Ex. 8
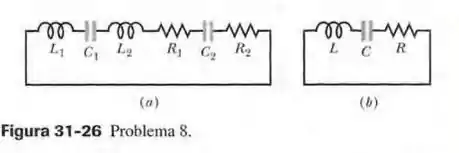
Um circuito com uma única malha é formado por indutores , capacitores e resistores , como, por exemplo, na Fig. 31-26a. Mostre que, qualquer que seja a sequência de elementos no circuito, o comportamento do circuito é idêntico ao do circuito LC simples da Fig. 31-26b. (Sugestão: considere a regra das malhas e veja o Problema 47 do Capítulo 30.)
Passo 1
E aí galerinha, vamos destruir essa questão comigo? Vamos láaaa!
Aplicando a lei das malhas ao circuito, temos:
Na qual
e . Este comportamento é equivalente ao do circuito simples da Fig. 31-26b.
Opa, gostou da resolução? Responde Aí!
Resposta
. Este comportamento é equivalente ao do circuito simples da Fig. 31-26b.
Exercícios de Livros Relacionados
Um capacitor de 1,50 μ F é ligado, como na Fig. 31-10, a um gerador de corrente alternada com E m = 30,0V . Determine a amplitude da corrente alternada resultante se a frequência da força eletromotriz
Em um circuito L C oscilante com C = 64,0 μ F , a corrente é dada por i = ( 1,60 ) s e n ( 2500 t + 0,680 ) , onde t está em segundos, i em ampères e a constante de fase em radianos. (a) Quanto temp
Um circuito série formado por uma indutância L 1 e uma capacitância C 1 oscila com uma frequência angular ω . Um segundo circuito série, contendo uma indutância L 2 e uma capacitância C 2 , oscila com
Qual é a capacitância de um circuito L C oscilante se a carga máxima do capacitor é 1,60 μ C e a energia total é 140 μ J ?
Em um circuito L C oscilante, a energia total é convertida de energia elétrica no capacitor em energia magnética no indutor em 1,50 μ s . Determine (a) o período das oscilações e (b) a frequência das