Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Halliday - Vol 3- Ed: 4º - Capítulo 36.Exercícios e Problemas - Ex. 16

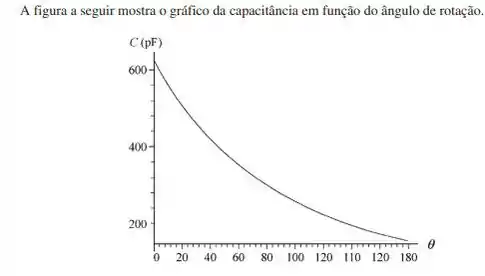
Um indutor é ligado a um capacitor cuja capacitância pode ser ajustada através de um botão. Queremos que a frequência deste circuito L C varie linearmente com o ângulo de rotação do botão, de 2 × 10 5   H z até 4 × 10 5   H z , quando o botão gira de 180 ∘ . Se L = 1,0 m H , plote a capacitância desejada C em função do ângulo de rotação do botão.

Passo 1

E aí galerinha, vamos destruir essa questão comigo? Vamos láaaa!

A relação linear entre  θ  (o ângulo de rotação do botão, em graus) e a frequência  f  deve ser

f = f 0 1 + θ 180 ∘ ⇒ θ = 180 ∘ f f 0 - 1

na qual f 0 = 2 × 10 5   H z . Como f = ω / 2 π = 1 / 2 π L C , podemos expressar a capacitância C em função de θ :

C = 1 4 π 2 L f 0 2 1 + θ / 180 ∘ 2 = 81 400.000 π 2 180 ∘ + θ 2

em unidade do SI ou, com a capacitância em picofarads,

C = 81 × 10 12 400.000 π 2 180 ∘ + θ 2 = 2,05 × 10 7 180 ∘ + θ 2

A figura a seguir mostra o gráfico da capacitância em função do ângulo de rotação.

Opa, gostou da resolução? Responde Aí!

Resposta

2,05 × 10 7 180 ∘ + θ 2

Exercícios de Livros Relacionados

APLICACAO EM ENGENMARIA A saida do retificador do Problema 56 pode ser filtrada adicionalmente conectando sua saida a um filtro passa-baixas como mostrado na Figura 29-39a.A saida resultante e uma ten
A tensao do gerador na Figura 29-40edada por S = ( 100 V) c o s ⁡ ( 2 π f t ) . a)Para cada ramo,qual e a corrente de pico e qual e a fase da corrente relativa a fase da tensao do gerador?(b)Na freque
APLICACAO EM ENGENHARIA Um metodo para determinar a compressibilidade de um material dieletrico usa um circuito LC com um capacitor de placas paralelas.O dieletricoinserido entre as placas e a variaca
Um circuito consiste em um gerador ac ideal,um capacitor e um indutor ideal,todos conectados em serie.A carga no capacitor edada por Q = 15 μ C cos ⁡ ω t + π 4 , onde ω = 1250 r a d s a)Determine a co
APUCACAO EM ENGENHARIA Ocircuito mostrado na Figura 29-37 e um filtro de corte.(Considere que a saida esteja conectada a uma carga que conduz uma corrente insignificante.)(a)Mostre que o filtro de cor