Circuitos que envolvem capacitores nem sempre podem ser agrupados em série e em pararelo. Como por exemplo, a Figura 24.39a mostra três capacitores, , e , formando uma ligação delta, assim chamada em virtuide de sua forma triangular. Essa ligação possui três terminais (a,b e c) e portanto não pode ser convertida e muma capacitância equivalente simples. Podemos mostrar que, desprezando qualquer efeito sobre circuitos externos, uma ligação delta é equivalente a uma circuito chamado de ligação . Por exemplo, a ligação delta indicada na Figura 24.39a pode ser substituída pela ligação indicada na Figura 24.39b. (O nome ligação também se refere à sua forma geométrica da ligação.) (a)Mostre que as equações de transformação que fornecem , e em função de e são dadas por
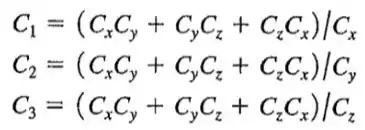
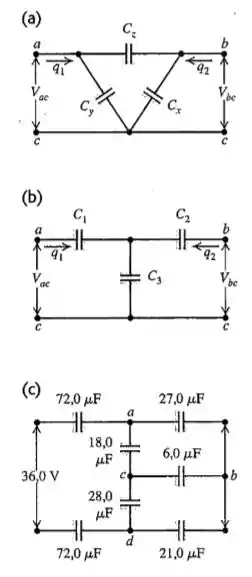
(Dica: As diferenças de potencial e devem ser as mesmas nos dois tipos de ligação. As cargas e que fluem nos sentidos indicados na Figura 24.39a devem ser as mesmas que as cargas e indicadas na Figura 24.39b. Obtenha uma relação para em função de e de e as capacitâncias envolvidas em cada circuito; e obtenha uma relação de em função das cargas para cada circuito. Os coeficientes das cargas correspondentes nas equações correspondentes devem ser iguais para os dois circuitos.) (b)Para o circuito indicado na Figura 24.39c, determine a capacitância equivalente entre os terminais do lado esquerdo do circuito. (Dica: Use a transformação delta-Y, deduzida na parte (a). Use os pontos a,b e c para formar a ligação delta e depois transforme a ligação delta na ligação Y. A seguir, os capacitores poderão ser combinados, usando-se as regras das ligações em série e em pararelo.) (c)Determine as cargas e as tensões de cada um dos capacitores indicados na Figura 24.39c.
Passo 1
Gente, eu sei que dá vontade de chorar... mas vamos lá! Essa questão nem é essas coisas apesar do texto infinito! Vamos lá! Primeiro, vamos transformar o circuito de delta para Y!
Passo 2
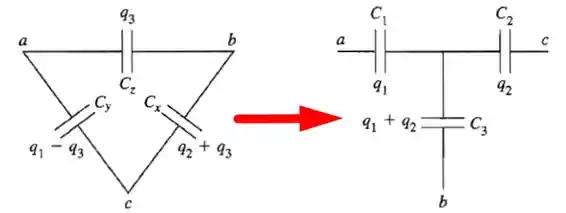
(a)Consideremos os dois circuitos mostrados na figura acima. Do circuito 1 (o da esquerda, temos que:
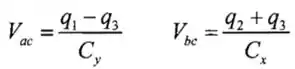
Temos também que é derivado de:
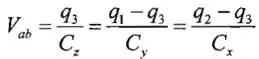
Isso nos dá:
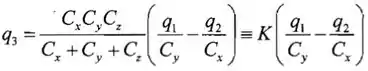
Legal? Do circuito 2 (o da direita), temos:
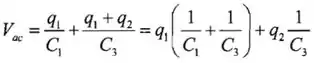
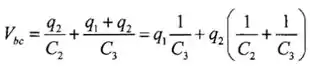
Estabelecendo os coeficientes das cargas iguais um ao outro em equações potenciais correspondentes dos dois circuitos em três equações independentes relacionando as duas capacitâncias. Essas equações são:
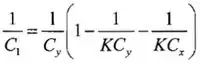
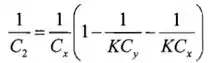
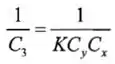
Desses, substituindo na expressão para , temos:
![]()
![]()
![]()
Passo 3
Ufa! Não podemos parar, vamos lá! (b) Usando a transformação do item (a), temos os circuitos equivalentes mostrados abaixo:
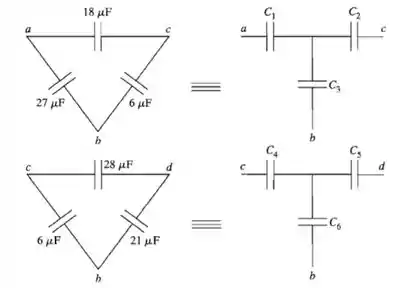
Temos que:
![]()
![]()
A capacitância equivalente total é de:
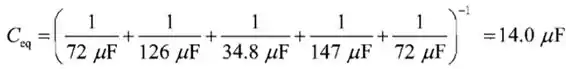
Onde, vem de:
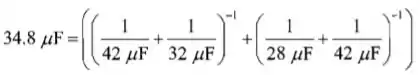
Passo 4
(c) O diagrama do circuito pode ser redesenhado na figura 25.73c. A carga total é dada por:
![]()
E isso é também a carga no capacitor de , portanto:
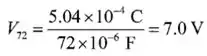
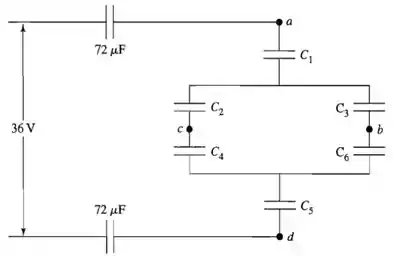
Agora encontraremos a tensão pelos capacitores numerados, e as tensões associadas a eles. Portanto essas tensões vão ser mudadas nas tensão original dos capacitores, e então as cargas deles:
![]()
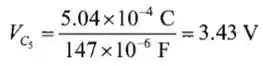
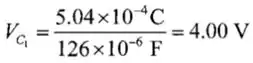
Portanto,
![]()
Mas,
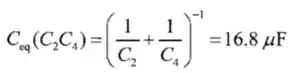
E,
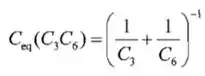
Logo,
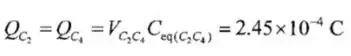
E,
![]()
Passo 5
E é isso, agora podemos calcular a tensão no capacitor 2,3, e 6!
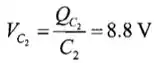
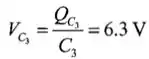
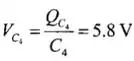
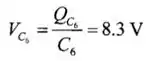
Temos também que:
![]()
E,
![]()
![]()
E,
![]()
Temos também que:
![]()
![]()
![]()
E,
![]()
![]()
E POR FIMMMMMM:
![]()
Resposta
Ei, a resposta está no passo a passo :)