Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 31.Problemas - Ex. 54

54 - O circuito R-L-C em paralelo. Um resistor, um indutor e um capacitor são ligados em paralelo com uma fonte CA com amplitude de voltagem V e frequência angular ω . Suponha que a voltagem da fonte seja dada por v = V cos ⁡ ω t .

  1. Mostre que a voltagem instantânea nos terminais de cada elemento V R , V L e V C em qualquer instante é a mesma da fonte v e que i = i R + i L + i C , em que i   é a corrente que passa na fonte i R , i L e i C são as correntes que passam no resistor, no indutor e no capacitor, respectivamente.
  2. Quais são as fases de i R , i L e i C em relação à v ? Use fasores para representar as correntes i , i R , i L e i C . Sobre o diagrama de fasores, mostre as fases dessas quatro correntes em relação a v .
  3. Use o diagrama de fasores do item (b) para mostrar que a amplitude da corrente I para a corrente i que passa na fonte é dada por I = I R 2 + I C - I L 2 .
  4. Mostre que o resultado da parte (c) pode ser escrito na forma I = V / Z , com 1 Z = 1 / R 2 + ω C - 1 / ω L 2

Passo 1

L e t r a   A :

Ora bolas, estamos falando de um circuito paralelo como esse daqui:

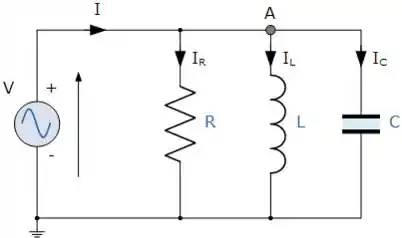
Perceba que de fato a tensão em cima de cada elemento é a tensão em cima da fonte V . Enquanto que pela lei das correntes, a corrente I tem que ser a soma das que passam pelos elementos:

I = I R + I L + I C

Passo 2

L e t r a   B :

Ora, a sabemos que a corrente que passa pelo indutor está sempre atrasado em relação a tensão de 90 ° , enquanto a corrente no indutor, sempre avante por 90 ° . No resistor, a tensão está em fase com a corrente!

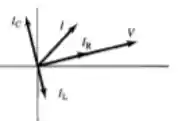
Veja que I C está 90 ° (perpendicular) avançado em relação à V , I L está na perpendicular, mas atrasado e I R em fase, ou seja, em cima de V . Veja também que I é a soma vetorial de todos eles!

Passo 3

L e t r a   C :

Como vimos e comentamos no passo anterior, a corrente I é a soma vetorial de todo mundo! O que vai ser dado por Pitágoras entre I R e I t :

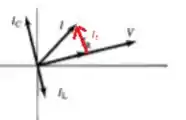
Então...

I = I R 2 + I t 2

Onde I t é a subtração de I C pela corrente do indutor que está para baixo:

I = I R 2 + I C - I L 2

Passo 4

L e t r a   D :

Bem, de fato a corrente I será dada pela Le de Ohm onde...

I = V Z

E esse Z é a impedância total do sistema:

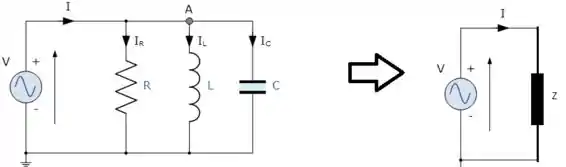
Podemos obter esse Z colocando todas as reatâncias em paralelo:

1 Z = 1 R + 1 - X c j + 1 X l j   →

Onde X c = 1 ω C e X l = ω L . Lembrando-se que 1 / j é - j ...

1 Z = 1 R + j 1 X c - j 1 X l   →

1 Z = 1 R + j ω C - j 1 ω L   →

O módulo dessa impedância então é...

1 Z = 1 R 2 + ω C - 1 ω L 2

Então, podemos concluir que a corrente será...

I = V Z =

V ⋅ 1 R 2 + ω C - 1 ω L 2

Sacou como faz?

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

74. Na Figura 30.32 , a chave é fechada, com o capacitor contendo a polaridade indicada. Determine o sentido (horário ou anti-horário) da corrente induzida na espira retangular A .
66. No circuito indicado na Figura 30.26 , a chave S está fechada há um longo tempo, o suficiente para que a leitura da corrente esteja estacionária a 3,50A . Subitamente, a chave S 2 é fechada, e a c
64. No circuito indicado na Figura 30.24 , a bateria e o indutor não possuem resistência interna significativa e não há corrente no circuito. Após a chave ser fechada, determine as leituras do amperím
70. Depois que a corrente na Figura 30.28 atinge seu valor estacionário final com a chave S 1 fechada e a chave S 2 aberta, a chave S 2 é fechada, colocando o indutor em curto-circuito. (A chave S 1 p
69. Considere o circuito indicado na Figura 30.28 . Seja ε = 36,0V , R 0 = 50,0Ω , R = 150,0Ω e L = 4,0H . ( a ) A chave S 1 é fechada e a chave S 2 é mantida aberta. Logo depois que a chave S 1 é fec