Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 93
Um clube automotivo planeja competir com um carro de na pista de corridas local. O carro precisa ser capaz de viajar ao redor de várias curvas de de raio a . Qual deveria ser o ângulo de inclinação das curvas para que a força do pavimento sobre os pneus seja na direção normal? Dica: O que essa exigência te diz sobre a força de atrito?
Passo 1
O que significa dizer que a força do pavimento sobre os pneus é normal? Quer dizer que queremos fazer a curva sem a ajuda da força de atrito.
Se houvesse força de atrito, haveria uma componente da força do pavimento na direção paralela ao chão.
Em outras palavras, a pista deve ser inclinada de forma que uma componente da força normal cumpra o papel de resultante centrípeta:
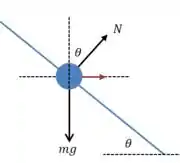
Vamos escrever a equação para nossa resultante centrípeta:
E na direção vertical, a outra componente de deve estar em equilíbrio com a força peso:
Passo 2
Ficamos então com o seguinte sistema:
Nosso objetivo é calcular o ângulo . Dividindo a primeira equação pela segunda, ficamos com o seguinte:
A rapidez é , ou , então:
Resposta
As curvas devem ter um ângulo de inclinação de .