Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 7.Problemas - Ex. 22
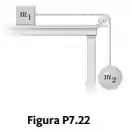
O coeficiente de atrito entre o bloco de massa m1 = 3,00 kg e a superfície na Figura P7.22 é k = 0,400. O sistema parte do repouso. Qual é a velocidade da bola de massa m2 = 5,00 kg quando ela já caiu uma distância h = 1,50 m?
Passo 1
Gente, pra gente saber essa velocidade, primeiro a gente tem que conhecer a aceleração com a qual a bola cai, que vai ser diferente da aceleração da gravidade , uma vez que está presa em uma corda, presa ao bloco de massa .
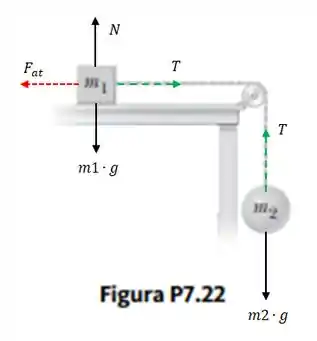
Pra isso, vamos começar pelos diagramas de corpo livre do bloco e da bola:
Passo 2
Vamos olhar primeiro pro bloco.
Como ele tá numa superfície plana, a força normal é igual ao peso dele, , então, por estarem ambas na mesma direção, se cancelam mutuamente.
Agora, como o exercício disse, o deslocamento se dá pra direita, então a força resultante no bloco tem o mesmo sentido da tração , e, por isso, a gente pode escrever a 2ª lei de Newton pro bloco assim:
Onde é a força de atrito e é a aceleração do bloco, que vai ser a mesma pra bola, pois estão amarrados pela corda, ok?
Bom, a gente sabe que e temos o valor de . Vamos aplicar tudo o que a gene já conhece nessa igualdade:
Como , a gente fica com isso:
Por fim :
Agora, avaliando as forças na bola, vamos descobrir o valor pra aceleração!
Passo 3
De novo, sendo a força resultante direcionada pra baixo, a gente pode escrever:
Aplicando os valores que a gente conhece:
Passo 4
Beleza, com essa igualdade e a última equação do Passo 2, a gente tem um sisteminha e, a partir dele, descobrimos ! Vamos fazer isso:
Maravilha! Essa vai ser a velocidade de queda da bola.
Passo 5
Como a bola cai do repouso, tem velocidade inicial . A gente quer descobrir a velocidade quando a bola cai uma altura de .
A gente consegue determinar isso com a equação de Torricelli, lembra??
Vamos aplicar nossos dados e determinar :