Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 8.2 - Ex. 28
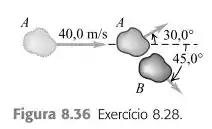
Colisão de asteróides. Dois asteróides de igual massa no cinturão entre Marte e Júpiter colidem entre si com um estouro luminoso. O asteróide , que se deslocava inicialmente a , é desviado em da sua direção original, enquanto o asteróide se desloca a da direção original de (Figura ).
a) Ache a velocidade escalar de cada asteróide após a colisão.
b) Qual fração da energia cinética original do asteróide se dissipa durante essa colisão?
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente encontrar (a) a velocidade de cada asteróide de massa após a colisão e (b) a fração de energia cinética original do asteróide , dissipada durante a colisão.
Antes de começarmos a responder as questões, por mais que já esteja representado na figura , acredito que a visualização da colisão não tenha ficado tão clara como deveria. Dessa forma, fazendo com que os asteroides sejam partículas e plotando a colisão em um plano cartesiano, teremos o seguinte:
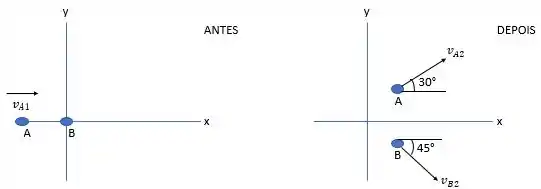
Com base nesses diagramas, vamos considerar o princípio da conservação do momento linear () para calcular a velocidade de cada asteróide. Depois vamos usar a relação , que representa o quociente entre a variação da energia cinética e a energia cinética inicial, para calcular a fração pedida. Vamos lá!
Passo 2
a) Sabendo que o momento se conserva para cada eixo separadamente, podemos escrever a lei de conservação do momento linear para cada eixo. Ademais, nossos termos são:
massa dos asteroides e ;
velocidade inicial do asteroide ;
velocidade inicial do asteroide ;
velocidade final do asteroide ;
velocidade final do asteroide .
Para o eixo , temos que a lei de conservação do momento linear será:
No qual é dado por . Sendo assim, teremos:
Note que os ângulos foram decompostos no eixo , que é o eixo que estamos tratando. Simplificando as massas (porque são iguais) e sabendo que o asteroide está em repouso inicialmente, então:
Substituindo os valores:
Passo 3
Para o eixo , temos que a lei de conservação do momento linear será:
No qual é dado por . Sendo assim, teremos:
Por que aparece esse sinal de menos? É porque o vetor velocidade está no quadrante do plano e a função seno é negativa nesse quadrante. É importante dar uma relembrada em trigonometria para fazer as questões de colisões, beleza? Continuando:
Substituindo a equação na , teremos o seguinte:
Passo 4
Substituindo esse valor que encontramos lá na equação , teremos:
Passo 5
b) Para descobrirmos essa fração de energia cinética dissipada, o que precisamos fazer é descobrir quanto vale a razão entre a variação de energia cinética do asteroide e a energia cinética inicial desse mesmo asteroide. Matematicamente, o que precisamos fazer é descobrir isso aqui ó:
Mas quem é ? Essa é a energia cinética final do asteroide , que é dada por:
E quem é esse ? Essa é a energia cinética inicial do asteroide , que é dada por:
Passo 6
Agora que encontramos as energias cinéticas, basta substituirmos naquela razão que fizemos ali em cima, se liga:
Simplificando os meios e a massa, teremos:
O sinal de negativo na porcentagem indica que esse valor foi dissipado durante a colisão.
Valeu, galera! Até a próxima! 😉
Resposta
a) e
b)