Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 3.Problemas - Ex. 48
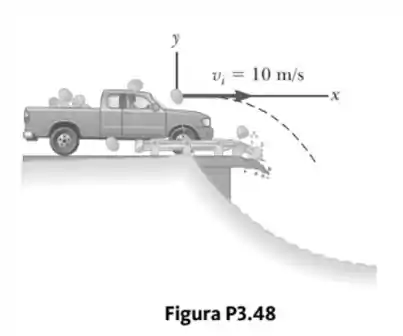
Um caminhão carregado de melancias para subitamente para evitar passar sobre a borda de uma ponte destruída (Fig. P3.48). A parada súbita faz que várias melancias voem para fora do caminhão. Uma delas sai do capô do caminhão com velocidade inicial na direção horizontal. Um corte transversal da margem tem a forma da metade inferior da parábola, com seu vértice na localização inicial da melancia projetada, com a equação , em que x e y são medidos em metros. Quais são as coordenadas x e y da melancia quando ela se espatifa na margem?
Passo 1
Então, gente, lembrando que a velocidade horizontal é sempre constante nesses lançamentos, como já vimos ao longo do capítulo, vale a gente escrever o seguinte:
Onde vai ser a distância horizontal alcançada pela melancia (o ponto onde ela se espatifa), e é o tempo de queda da fruta. A situação é mais ou menos essa:
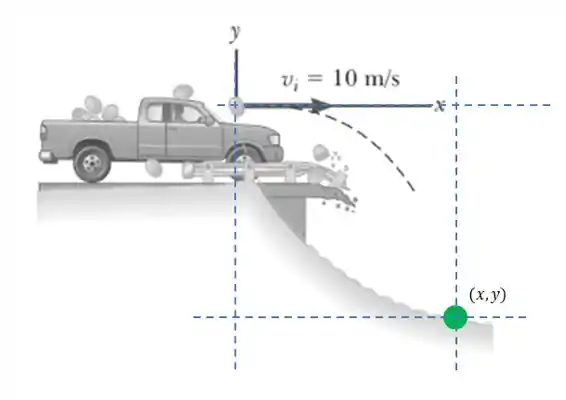
Beleza? Só que a gente sabe a relação entre e dada pela equação da parábola, sendo:
Então, a gente tira daqui que a distância vertical (pra baixo) atingida pela melancia foi , beleza? Guarda essas infos pra gente usar mais na frente!
Passo 2
Bom, e como dá pra gente achar uma expressão pro tempo ?
Repara, avaliando agora a trajetória na vertical da melancia, ela cai com velocidade (vertical) nula. E como toda queda é acelerada, o melhor aqui é usar a equação do sorvetão:
Pro nosso caso, é a posição vertical final, que pro esquema da parábola que a gente tá avaliando, a gente pode chamar de posição , portanto ;
é a posição de onde a melancia parte desde a queda, que é dado no enunciado como o vértice da parábola, ou seja, o ponto . Nisso, ;
a gente acabou de ver que vale zero também, e a aceleração é a gravidade, que podemos considerar aqui sendo .
Beleza, aplicando nossos valores, a gente tem:
Passo 3
Legal?
Agora a gente tem duas equações que correlacionam e , vamos então trabalhar elas pra determinar nossas incógnitas!
A gente tem:
E
Vamos elevar ambos os lados da equação debaixo ao quadrado, obtendo:
Agora, da primeira equação, substituímos por e aplicamos na última expressão. Vamos ter:
Simplificamos os fatores e isolando:
Passo 4
Com isso, gente, determinamos e :
E, por fim, :
Resposta
e