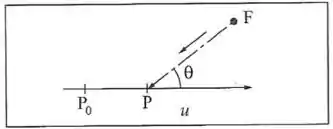
Complete a teoria do efeito Doppler para movimento numa direção qualquer calculando a frequência percebida por um observador quando a fonte, de frequência , está em repouso na atmosfera e o observador se move ao longo de uma direção com velocidade de magnitude . No instante considerado, a direção que liga o observador à fonte (figura) faz um ângulo com a direção do movimento. Verifique se recai nos resultados obtidos no texto para e .

Vamos começar desenhando e calculando o caso em que (que é o caso tradicional):

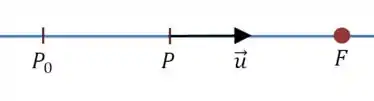
A fórmula geral para o efeito Doppler é:

Nesse caso temos e :

E como estamos falando de uma aproximação, precisamos ter , então o sinal no numerador tem que ser positivo:

Agora vamos ver o que acontece quando a trajetória da fonte é desviada por um ângulo :

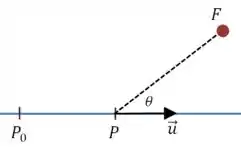
A única diferença é que a velocidade de aproximação vai mudar. Temos que projetar o vetor na direção .

Então:

E quando nós voltamos ao caso inicial.

Quando , a fonte está atrás do observador, e portanto ocorre afastamento:

Ou seja, o sinal do numerador se torna negativo, exatamente como deveria ser.