Enunciado
Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 16.Exercício - Ex. 43
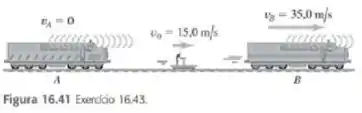
Dois trens, A e B, apitam simultaneamente com a mesma frequência de . O trem A está em repouso e o trem B se desloca para a direita (se afastando de A) com velocidade igual a . Um ouvinte esta entre os dois apitos e se desloca para a direita com velocidade de (Figura 16.41). não existe vento. a) qual é a frequência que o ouvinte escuta do apito de A? b) Qual é a frequência que ele escuta de B? c) Qual é a frequência dos batimentos que o ouvinte escuta?
Passo 1
Nas duas primeiras letras, vamos usar a equação do efeito Doppler:
Vamos considerar para os dois casos que o sentido positivo é do ouvinte para a fonte. Na letra (a) a equação ficará o seguinte:
O sinal negativo de aparece por causa da consideração que fizemos, já que o som se desloca da fonte para o ouvinte ( o ouvinte se afasta da onda).
Passo 2
Na (b), a gente usa novamente a equação do efeito Doppler:
Dessa vez os sinais das velocidades tanto da fonte quanto do ouvinte serão positivas, pois a fonte que se afasta do ouvinte:
Passo 3
(c) Agora que temos as duas frequências, basta suarmos a equação de batimento:
Para calcularmos o batimento ouvido pelo ouvinte: