Enunciado
Física - Young and Freedman - Vol 3- Ed: 14º - Capítulo 32.Exercícios - Ex. 41
Um condutor cilíndrico com seção reta circular de raio a e resistividade r conduz uma corrente constante I. (a) Determine o módulo, a direção e o sentido do vetor em um ponto imediatamente abaixo da superfície do fio situado a uma distância a do eixo central. (b) Determine o módulo, a direção e o sentido do vetor nesse mesmo ponto. (c) Calcule o módulo, a direção e o sentido do vetor de Poynting nesse mesmo ponto. (O sentido de indica o sentido em que a energia eletromagnética flui para o interior ou para o exterior do condutor.) (d) Use o resultado do item (c) para calcular a taxa de escoamento de energia para o interior do volume ocupado por um comprimento l do condutor. (Dica: integre sobre a superfície do volume considerado.) Compare o resultado à taxa da geração de energia térmica no mesmo volume. Explique por que a energia dissipada na resistência de um condutor que conduz uma corrente pode ser interpretada em termos de uma energia que penetra no solenoide através de suas paredes cilíndricas.
Passo 1
E aiii gente,
Tudo bom com vocês?
Vamos fazer mais uma questãozinha aqui!
Letra a:
A direção de é paralela ao eixo do cilindro, na direção da corrente. Então,
(E é uniforme em toda a seção transversal do condutor.)
Passo 2
Letra b:
Uma vista em corte transversal do condutor é dada na figura abaixo:
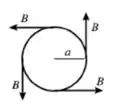
Seja a corrente saindo da página.
Aplique a lei de Ampère a um círculo de raio a.
nos dá:
E
A direção de é no sentido anti-horário ao redor do círculo.
Passo 3
Letra c:
As direções de são mostradas na figura abaixo:
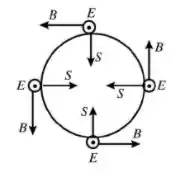
A direção de é radialmente para dentro.
Resposta
- A direção de é no sentido anti-horário ao redor do círculo.