Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 21.Problemas - Ex. 78
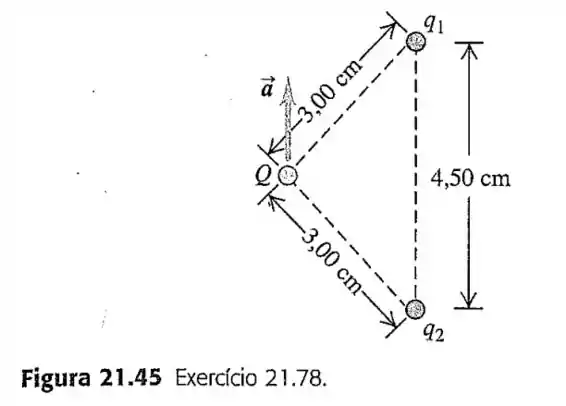
78- Duas cargas puntiforme e são mantidas fixas a uma distância de . Outra carga puntiforme , de massa igual a , está inicialmente localizada a de cada uma dessas cargas (Figura ) e é libertada do repouso. Você verifica que a aceleração inicial de é de baixo para cima, paralela a linha que liga as duas cargas puntiformes. Ache e .
Passo 1
Como foi nos dada a massa de e a aceleração de então podemos achar a força em de forma que ela valha:
E essa força aponta na mesma direção da aceleração. Agora vamos desenhar as forças que as partículas e agem na partícula .
Passo 2
Sabendo que a carga e para que haja uma força para cima a partícula deve repelir a partícula , portanto ter uma carga negativa e a carga deve atrair a carga e para que não haja nenhuma componente na horizontal então as duas cargas devem ser iguais (afinal a distância em do eixo é igual.
Dessa forma por ter a mesma distância e a mesma carga então , então a somatória das forças verticais será:
Pois o ângulo é o mesmo ângulo da distância entre a partícula e o eixo vertical.
Passo 3
Então a carga de uma dessas partículas menores será calculada por:
E como visto no passo 1 a carga deve ser negativa e a carga deve ser positiva e ambas tem o mesmo módulo pois se eles forem diferentes nós teríamos uma componente em .