Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 29.2 - Ex. 2

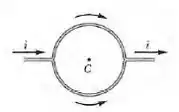
Um condutor retilíneo percorrido por uma corrente se divide em dois arcos semicirculares, como mostra a figura 29-35. Qual o campo magnético no centro C da espira circular resultante?

Passo 1

Fala aí! tudo certinho? 😊

Nesse problema temos um condutor retilíneo percorrido por uma corrente se divide em dois arcos semicirculares. A partir daí queremos saber qual o campo magnético no centro C da espira circular resultante.

Parece complicado? 🤔

Para encontrarmos o campo magnético no ponto C podemos aplicar a lei de Biot-Savart ao fio. Relembrando a lei é a seguinte:

Quando tratamos de arcos de circunferência, a equação de Biot-Savart se transforma em

onde é o ângulo central do arco em questão.

Veja só! 😁

Passo 2

Na nossa questão, , em cada semicirculo. Substituindo na equação, vamos calcular o campo para o semicírculo superior.

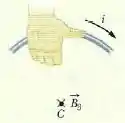
Para determinar a orientação do campo, vamos aplicar a regra da mão direita como mostra a figura a seguir.

Vamos segurar o arco mentalmente com a mão direita, com o polegar apontando para o sentio da corrente.

Os outros dedos da sua mão indicam a orientação do campo magnética nas vizinhanças do fio. Na região do ponto C, os dedos apontam para dentro do papel.

Passo 3

Agora vamos calcular o campo para o semicirculo inferior!

Os campos são iguais em módulo mas será que o segundo também possui a mesma orientação do primeiro? Vamos descobrir aplicando a regra da mão direita também!

Vamos segurar o arco mentalmente com a mão direita, com o polegar apontando para o sentio da corrente.

Os outros dedos da sua mão indicam a orientação do campo magnética nas vizinhanças do fio. Na região do ponto C, os dedos apontam para fora do papel.

Ou seja, como a contribuição do semicirculo superior é contrária a do círculo inferior e de mesmo módulo, o campo resultante no ponto C é igual a zero!

E aí! entendeu tudo? Responde Aí! 😉